
题目列表(包括答案和解析)
 表示相等函数。其中正确命题的个数是( )
表示相等函数。其中正确命题的个数是( ) 与x轴没有交点,则
与x轴没有交点,则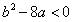 且a>0;
且a>0; 的递增区间为
的递增区间为 ;(4)y=1+x和
;(4)y=1+x和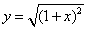 表示相等函数。
表示相等函数。下列说法不正确的是
A.“ ”的否定是“
”的否定是“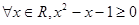 ”
”
B.命题“若x>0且y>0,则x +y>0”的否命题是假命题
C. 满足x1<1<x2”和“函数
满足x1<1<x2”和“函数
 在[1,2]上单调递增”同时为真
在[1,2]上单调递增”同时为真
D.△ABC中A是最大角,则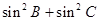 <sin2A是△ABC为钝角三角形的充要条件
<sin2A是△ABC为钝角三角形的充要条件
下列说法不正确的是( )
A.“ ”的否定是“
”的否定是“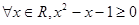 ”
”
B.命题“若x>0且y>0,则x +y>0”的否命题是假命题
C. 满足x1<1<x2”和“函数
满足x1<1<x2”和“函数 在[1,2]上单调递增”同时为真
在[1,2]上单调递增”同时为真
D.△ABC中,A是最大角,则 <sin2A是△ABC为钝角三角形的充要条件.
<sin2A是△ABC为钝角三角形的充要条件.
一、选择题(每小题5分,共计60分)
ABADD CACAC AB
二、填空题(每小题4分,共计16分)
(13)4;(14) ;(15)
;(15) ;(16)①④.
;(16)①④.
三、解答题:
17.解:(本小题满分12分)
(Ⅰ) 由题意



由题意,函数周期为3 ,又
,又 >0,
>0, ;
;
(Ⅱ) 由(Ⅰ)知


又x ,
,
 的减区间是
的减区间是 .
.
(18) (本小题满分12分)
解:(1)随机变量 的所有可能取值为
的所有可能取值为






所以随机变量 的分布列为
的分布列为

0
1
2
3
4
5







(2)∵随机变量
∴
19. (本小题满分12分)
解:(Ⅰ) ∵ 底面ABCD是正方形,
∵ 底面ABCD是正方形,
∴AB⊥BC,
又平面PBC⊥底面ABCD
平面PBC ∩ 平面ABCD=BC
∴AB ⊥平面PBC
又PC 平面PBC
平面PBC
∴AB ⊥CP ………………3分
(Ⅱ)解法一:体积法.由题意,面 面
面 ,
,
取 中点
中点 ,则
,则
 面
面 .
.
再取 中点
中点 ,则
,则 ………………5分
………………5分
设点 到平面
到平面 的距离为
的距离为 ,则由
,则由



 .
………………7分
.
………………7分
 解法二:
解法二: 面
面
取 中点
中点 ,再取
,再取 中点
中点

 ,
,


过点 作
作 ,则
,则
在 中,
中,
由
∴点 到平面
到平面 的距离为
的距离为 。 ………………7分
。 ………………7分
解法三:向量法(略)
(Ⅲ)
 面
面


 就是二面角
就是二面角 的平面角.
的平面角.


∴二面角 的大小为45°. ………………12分
的大小为45°. ………………12分
方法二:向量法(略).
(20)(本小题满分12分)
解:(Ⅰ)方法一:∵ ,
,
∴ .
.
设直线 ,
,
并设l与g(x)=x2相切于点M( )
)
∵
 ∴2
∴2
∴
代入直线l方程解得p=1或p=3.
方法二:
将直线方程l代入  得
得

∴
解得p=1或p=3 .
(Ⅱ)∵ ,
,
①要使 为单调增函数,须
为单调增函数,须 在
在 恒成立,
恒成立,
即 在
在 恒成立,即
恒成立,即 在
在 恒成立,
恒成立,
又 ,所以当
,所以当 时,
时, 在
在 为单调增函数; …………6分
为单调增函数; …………6分
②要使 为单调减函数,须
为单调减函数,须 在
在 恒成立,
恒成立,
即 在
在 恒成立,即
恒成立,即 在
在 恒成立,
恒成立,
又 ,所以当
,所以当 时,
时, 在
在 为单调减函数.
为单调减函数.
综上,若 在
在 为单调函数,则
为单调函数,则 的取值范围为
的取值范围为 或
或 .………8分
.………8分
(21) (本小题满分12分)
(1)∵直线 的方向向量为
的方向向量为
∴直线 的斜率为
的斜率为 ,又∵直线
,又∵直线 过点
过点
∴直线 的方程为
的方程为
∵ ,∴椭圆的焦点为直线
,∴椭圆的焦点为直线 与
与 轴的交点
轴的交点
∴椭圆的焦点为
∴ ,又∵
,又∵
∴ ,∴
,∴
∴椭圆方程为
(2)设直线MN的方程为
由 ,
, 得
得

设 坐标分别为
坐标分别为
则
 (1)
(1)  (2)
(2)
 >0
>0
∴
 ,
,
∵ ,显然
,显然 ,且
,且
∴
∴
代入(1) (2),得


∵
 ,得
,得
 ,即
,即

解得 且
且 .
.
(22) (本小题满分14分)
(1) 解:过 的直线方程为
的直线方程为
联立方程 消去
消去 得
得

∴
即
(2)
∴ 是等比数列
是等比数列
 ,
, ;
;
(III) 由(II)知,
由(II)知, ,要使
,要使 恒成立由
恒成立由
 =
= >0恒成立,
>0恒成立,
即(-1)nλ>-( )n-1恒成立.
)n-1恒成立.
?。当n为奇数时,即λ<( )n-1恒成立.
)n-1恒成立.
又( )n-1的最小值为1.∴λ<1. 10分
)n-1的最小值为1.∴λ<1. 10分
?。当n为偶数时,即λ>-( )n-1恒成立,
)n-1恒成立,
又-( )n-1的最大值为-
)n-1的最大值为- ,∴λ>-
,∴λ>- . 11分
. 11分
即- <λ<1,又λ≠0,λ为整数,
<λ<1,又λ≠0,λ为整数,
∴λ=-1,使得对任意n∈N*,都有 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com