
题目列表(包括答案和解析)
(12分)已知二次函数
(Ⅰ)若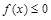 的解集为
的解集为 求实数
求实数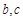 的值;
的值;
(Ⅱ)若 满足
满足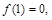 且关于
且关于 的方程
的方程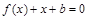 的两个实数根分别在区间(-3,-2),(0,1)内,求实数
的两个实数根分别在区间(-3,-2),(0,1)内,求实数 的取值范围.
的取值范围.
已知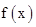 是二次函数,不等式
是二次函数,不等式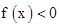 的解集是(0,5),且f(x)在区间[-1,4]上的最大值是12.
的解集是(0,5),且f(x)在区间[-1,4]上的最大值是12.
(1)求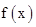 的解析式;
的解析式;
(2)是否存在自然数m,使得方程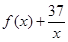 =0在区间(m,m+1)内有且只有两个不等的实数根?若存在,求出所有m的值;若不存在,请说明理由.
=0在区间(m,m+1)内有且只有两个不等的实数根?若存在,求出所有m的值;若不存在,请说明理由.
已知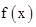 是二次函数,不等式
是二次函数,不等式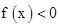 的解集是(0,5),且f(x)在区间[-1,4]上的最大值是12.
的解集是(0,5),且f(x)在区间[-1,4]上的最大值是12.
(1)求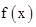 的解析式;
的解析式;
(2)是否存在自然数m,使得方程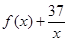 =0在区间(m,m+1)内有且只有两个不等的实数根?若存在,求出所有m的值;若不存在,请说明理由.
=0在区间(m,m+1)内有且只有两个不等的实数根?若存在,求出所有m的值;若不存在,请说明理由.
 是二次函数,不等式
是二次函数,不等式 的解集是(0,5),且f(x)在区间[-1,4]上的最大值是12.
的解集是(0,5),且f(x)在区间[-1,4]上的最大值是12. 的解析式;
的解析式; =0在区间(m,m+1)内有且只有两个不等的实数根?若存在,求出所有m的值;若不存在,请说明理由.
=0在区间(m,m+1)内有且只有两个不等的实数根?若存在,求出所有m的值;若不存在,请说明理由. )=
)= 在区间(0,π)内的解集 .
在区间(0,π)内的解集 .一、 填空题:
1、 2、
2、 3、128 4、
3、128 4、 5、64 6、
5、64 6、
7、 8、
8、 9、-4 10、15 11、
9、-4 10、15 11、
12、(1)(2)(5)
二、选择题:
13、D 14、 C 15、 B 16、 C
17、解:以A为原点,以AB、AD、AP所在直线分别 轴,
轴,
建立空间直角坐标系。 -----2分
则 C(2,1,0) N(1,0,1)  =(-1,-1,1)---4分
=(-1,-1,1)---4分
D(0,2,0) M(1, ,1)
,1)  =(1,-
=(1,- ,1)---6分
,1)---6分
设 与
与 的夹角为
的夹角为 ,
,
 ----8分
----8分
 ---10分
---10分
 异面直线
异面直线 与
与 所成的角为
所成的角为 -----12分
-----12分
18、解:延长 ,作
,作 交
交 于D,------4分
于D,------4分
设 ,则
,则
 ------8分
------8分
解得 .------10分
.------10分
故船继续朝原方向前进有触礁的危险.-----12
19、解: (1)因为f(x+y)=f(x)+f(y),
令x=y=0,代入①式,-----2分
得f(0+0)=f(0)+f(0),即 f(0)=0 --------4分
(2)令y=-x,代入①式,得 f(x-x)=f(x)+f(-x),又f(0)=0,
则有0=f(x)+f(-x).------6分
即f(-x)=-f(x)对任意x∈R成立,
所以f(x)是奇函数.......8分
(3) f(3)=log 3>0,即f(3)>f(0),
3>0,即f(3)>f(0),
又f(x)在R上是单调函数,所以f(x)在R上是增函数,----10分
又由(1)f(x)是奇函数.
f(k?3 )<-f(3
)<-f(3 -9
-9 -2)=f(-3
-2)=f(-3 +9
+9 +2),
+2),
k?3 <-3
<-3 +9
+9 +2,
+2,
得 ------12分
------12分

 ------------14分
------------14分
20、解:(1) 为等差数列,∵
为等差数列,∵ ,又
,又 ,
,
∴  ,
, 是方程
是方程 的两个根
的两个根
又公差 ,∴
,∴ ,∴
,∴ ,
, -------- 2分
-------- 2分
∴  ∴
∴ ∴
∴ -----------4分
-----------4分
(2)由(1)知, -----------5分
-----------5分
∴
∴ ,
, ,
, ------------7分
------------7分
∵ 是等差数列,∴
是等差数列,∴ ,∴
,∴ ----------8分
----------8分
∴ (
( 舍去)
------------9分
舍去)
------------9分
(3)由(2)得 -------------11分
-------------11分
 ,
, 时取等号 ------- 13分
时取等号 ------- 13分
 ,
, 时取等号15分
时取等号15分
(1)、(2)式中等号不可能同时取到,所以 -----------16分
-----------16分
21、解:(1)椭圆 与
与 相似. -----2分
相似. -----2分
因为 的特征三角形是腰长为4,底边长为
的特征三角形是腰长为4,底边长为 的等腰三角形,
的等腰三角形,
而椭圆 的特征三角形是腰长为2,
的特征三角形是腰长为2,
底边长为 的等腰三角形,
的等腰三角形,
因此两个等腰三角形相似,且相似比为 .
---
6分
.
---
6分
(2)椭圆 的方程为:
的方程为: .
--------8分
.
--------8分
假定存在,则设 、
、 所在直线为
所在直线为 ,
, 中点为
中点为 .
.
则
 .
-------10分
.
-------10分
所以 .
.
中点在直线 上,所以有
上,所以有 . ----12分
. ----12分
 .
.
 . -------14分
. -------14分
(3)椭圆 的方程为:
的方程为: .
.
两个相似椭圆之间的性质有: 写出一个给2分
① 两个相似椭圆的面积之比为相似比的平方;
② 分别以两个相似椭圆的顶点为顶点的四边形也相似,相似比即为椭圆的相似比;
③ 两个相似椭圆被同一条直线所截得的线段中点重合;
过原点的直线截相似椭圆所得线段长度之比恰为椭圆的相似比. ----20分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com