
题目列表(包括答案和解析)
在函数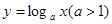 的图象上有
的图象上有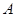 、
、 、
、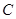 三点,横坐标分别为
三点,横坐标分别为 其中
其中 .
.
⑴求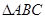 的面积
的面积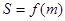 的表达式;
的表达式;
⑵求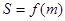 的值域.
的值域.
【解析】由题意利用分割可先表示三角形ABC的面积,然后应用对数运算性质及二次函数的性质求解函数的最大值,属于知识的简单综合.
如图,D,E分别是△ABC边AB,AC的中点,直线DE交△ABC的外接圆与F,G两点,若CF∥AB,证明:

(Ⅰ) CD=BC;
(Ⅱ)△BCD∽△GBD.
【命题意图】本题主要考查线线平行判定、三角形相似的判定等基础知识,是简单题.
【解析】(Ⅰ) ∵D,E分别为AB,AC的中点,∴DE∥BC,
∵CF∥AB, ∴BCFD是平行四边形,
∴CF=BD=AD, 连结AF,∴ADCF是平行四边形,

∴CD=AF,
∵CF∥AB, ∴BC=AF, ∴CD=BC;
(Ⅱ) ∵FG∥BC,∴GB=CF,
由(Ⅰ)可知BD=CF,∴GB=BD,
∵∠DGB=∠EFC=∠DBC, ∴△BCD∽△GBD
若定义在D上的函数y=f(x)满足条件:存在实数a,b(a<b)且![]()
![]()
![]() ,使得:(1)任取x0∈[a,b],有f(x0)=C(C是常数);(2)对于D内任意y0,当y0
,使得:(1)任取x0∈[a,b],有f(x0)=C(C是常数);(2)对于D内任意y0,当y0![]() [a,b],总有f(y0)<C.我们将满足上述两条件的函数f(x)称为“平顶型”函数,称C为“平顶高度”,称b-a为“平顶宽度”.根据上述定义,解决下列问题:
[a,b],总有f(y0)<C.我们将满足上述两条件的函数f(x)称为“平顶型”函数,称C为“平顶高度”,称b-a为“平顶宽度”.根据上述定义,解决下列问题:
(1)函数f(x)=-|x+2|-|x-3|是否为“平顶型”函数?若是,求出“平顶高度”和“平顶宽度”;若不是,简要说明理由.
(2)已知![]() 是“平顶型”函数,求出m,n的值.
是“平顶型”函数,求出m,n的值.
(3)对于(2)中的函数f(x),若f(x)=kx在x∈[-2,+∞)上有两个不相等的根,求实数k的取值范围.
若定义在D上的函数y=f(x)满足条件:存在实数a,b(a<b)且[a,b]![]() D,使得:(1)任取x0∈[a,b],有f(x0)=C(C是常数);
D,使得:(1)任取x0∈[a,b],有f(x0)=C(C是常数);
(2)对于D内任意y0,当y0![]() [a,b],总有f(y0)<C.
[a,b],总有f(y0)<C.
我们将满足上述两条件的函数f(x)称为“平顶型”函数,称C为“平顶高度”,称b-a为“平顶宽度”.根据上述定义,解决下列问题:
(1)函数f(x)=-|x+2|-|x-3|是否为“平顶型”函数?若是,求出“平顶高度”和“平顶宽度”;若不是,简要说明理由.
(2)求实数n的值,使函数![]() 是“平顶型”函数.
是“平顶型”函数.
(3)对于(2)中的函数f(x),若f(x)=kx在x∈[-2,+∞)上有两个不相等的根,求实数k的取值范围.
已知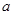 ,
,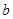 ,
,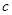 分别为
分别为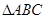 三个内角
三个内角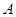 ,
,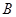 ,
,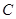 的对边,
的对边, .
.
(Ⅰ)求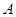 ;
;
(Ⅱ)若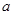 =2,
=2,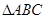 的面积为
的面积为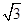 ,求
,求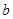 ,
,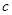 .
.
【命题意图】本题主要考查正余弦定理应用,是简单题.
【解析】(Ⅰ)由 及正弦定理得
及正弦定理得
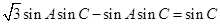
由于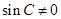 ,所以
,所以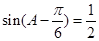 ,
,
又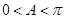 ,故
,故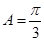 .
.
(Ⅱ) 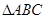 的面积
的面积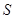 =
=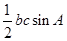 =
=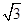 ,故
,故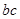 =4,
=4,
而 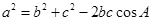 故
故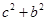 =8,解得
=8,解得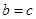 =2
=2
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com