
题目列表(包括答案和解析)
(1)求f(x)的单调区间;
(2)讨论f(x)的极值.
所以f(-1)=2是极大值,f(1)=-2是极小值.
(2)曲线方程为y=x3-3x,点A(0,16)不在曲线上.
设切点为M(x0,y0),则点M的坐标满足y0=x03-3x0.
因f′(x0)=3(x02-1),故切线的方程为y-y0=3(x02-1)(x-x0).
注意到点A(0,16)在切线上,有16-(x03-3x0)=3(x02-1)(0-x0),
化简得x03=-8,解得x0=-2.
所以切点为M(-2,-2),
切线方程为9x-y+16=0.
| C | 0 n |
| C | 1 n |
| C | 2 n |
| C | n n |
| C | 2 n |
| C | 3 n |
| C | 4 n |
| C | n n |
| C | 1 n |
| C | 2 n |
| C | 3 n |
| C | n n |
| C | 2 n |
| C | 3 n |
| C | 4 n |
| C | n n |
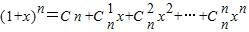 (x∈R,整数n≥2),证明:
(x∈R,整数n≥2),证明: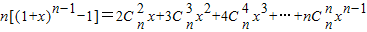 ;
; 的值;
的值;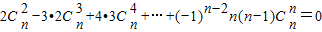 .
.| C | 0n |
| C | 1n |
| C | 2n |
| C | nn |
| C | 2n |
| C | 3n |
| C | 4n |
| C | nn |
| C | 1n |
| C | 2n |
| C | 3n |
| C | nn |
| C | 2n |
| C | 3n |
| C | 4n |
| C | nn |
若x∈(8,10),则化简![]() 得 ( )
得 ( )
A 2x-18 B 2 C 18-2x D -2
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com