
题目列表(包括答案和解析)


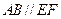

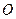
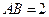

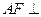 平面
平面 ;
;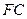 的中点为
的中点为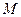 ,求证:
,求证: 平面
平面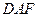 ;
; 的体积.
的体积.| OC |
| OA |
| OB |
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| a2 |
| 1 |
| b2 |
| OC |
| OM |
| ON |
| OA |
| OB |
| OP |
| OA1 |
| OA2 |
| OP |
| OA1 |
| OA2 |
| OAn |
| OP |
| OA1 |
| OA2 |
| OAn |
| OP |
| OA1 |
| OA2 |
| OAn |
| OC |
| OM |
| ON |
| OA |
| OB |
(一)
【解题思路】:设f(x)的二次项系数为m,其图象上两点为(1-x,有详细的答案或解析.files/image196.gif) )、B(1+x,
)、B(1+x,有详细的答案或解析.files/image198.gif) )因为
)因为有详细的答案或解析.files/image200.gif) ,
,有详细的答案或解析.files/image006.gif) ,所以
,所以有详细的答案或解析.files/image203.gif) ,由x的任意性得f(x)的图象关于直线x=1对称, ………………………………………………………………(2分)
,由x的任意性得f(x)的图象关于直线x=1对称, ………………………………………………………………(2分)
∵ 有详细的答案或解析.files/image205.gif) ,
,有详细的答案或解析.files/image207.gif) ,
,有详细的答案或解析.files/image209.gif) ,
,
有详细的答案或解析.files/image211.gif) ,
,有详细的答案或解析.files/image213.gif) ,
,有详细的答案或解析.files/image215.gif)
有详细的答案或解析.files/image217.gif) ,………………………………(4分)
,………………………………(4分)
∴ 当有详细的答案或解析.files/image219.gif) 时,∵f(x)在x≥1内是增函数,
时,∵f(x)在x≥1内是增函数,
有详细的答案或解析.files/image221.gif)
有详细的答案或解析.files/image223.gif)
有详细的答案或解析.files/image225.gif)
有详细的答案或解析.files/image227.gif)
有详细的答案或解析.files/image229.gif)
有详细的答案或解析.files/image231.gif) ,
,有详细的答案或解析.files/image233.gif) .
.
∵ 有详细的答案或解析.files/image235.gif) , ∴
, ∴ 有详细的答案或解析.files/image237.gif) .………………………………………………(8分)
.………………………………………………(8分)
当有详细的答案或解析.files/image239.gif) 时,∵f(x)在x≥1内是减函数.
时,∵f(x)在x≥1内是减函数.
同理可得有详细的答案或解析.files/image241.gif) 或
或有详细的答案或解析.files/image243.gif) ,
,有详细的答案或解析.files/image233.gif) .………………………………………(11分)
.………………………………………(11分)
综上:有详细的答案或解析.files/image245.gif) 的解集是当
的解集是当有详细的答案或解析.files/image219.gif) 时,为
时,为有详细的答案或解析.files/image248.gif)
当有详细的答案或解析.files/image239.gif) 时,为
时,为有详细的答案或解析.files/image251.gif) ,或
,或有详细的答案或解析.files/image253.gif) .…………………………(12分)
.…………………………(12分)
【试题评析】:本小题主要考查最简单三角不等式的解法等基本知识,涉及到分类讨论、二次函数的对称性、向量的数量积、函数的单调性等基本知识和方法的综合运用,考查运算能力及逻辑思维能力。
18.(理)【解题思路】:(1)设甲队在第五场比赛后获得冠军为事件M,则第五场比赛甲队获胜,前四场比赛甲队获胜三场,
依题意得有详细的答案或解析.files/image255.gif) .……………………………(6分)
.……………………………(6分)
(2)设甲队获得冠军为事件E,则E包含第四、第五、第六、第七场获得冠军四种情况,且它们彼此互斥.
∴ 有详细的答案或解析.files/image257.gif) .
.
………………………………………………………………(12分)
【试题评析】:考查互斥事件有一个发生的概率,相互独立事件同时发生的概率,n次独立重复实验恰好k次发生的概率。考查逻辑思维能力,要求考生具有较强的辨别雷同信息的能力。
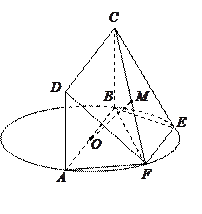
19.【解题思路】:解法一:(1)取PC中点M,连结ME、MF,则MF∥CD,MF=有详细的答案或解析.files/image012.gif) CD,又AE∥CD,AE=
CD,又AE∥CD,AE=有详细的答案或解析.files/image012.gif) CD,∴AE∥MF,且AE=MF,∴四边形AFME是平行四边形,∴AF∥EM,∵AF
CD,∴AE∥MF,且AE=MF,∴四边形AFME是平行四边形,∴AF∥EM,∵AF有详细的答案或解析.files/image261.gif) 平面PCE,∴AF∥平面PCE.
…………………………………(4分)
平面PCE,∴AF∥平面PCE.
…………………………………(4分)
(2)∵PA⊥平面ABCD,CD⊥AD. ∴CD⊥PD,∴∠PDA是二面角P-CD-B的平面角,即∠PDA=45°, ………………………………………………………………(6分)
∴△PAD是等腰直角三角形,∴AF⊥PD,又AF⊥CD,∴AF⊥平面PCD,而EM∥AF,∴EM⊥平面PCD.
又EM有详细的答案或解析.files/image263.gif) 平面PEC,∴面PEC⊥面PCD.
在平面PCD内过F作FH⊥PC于H,则FH就是点F到平面PCE的距离.
…………………………………(10分)
平面PEC,∴面PEC⊥面PCD.
在平面PCD内过F作FH⊥PC于H,则FH就是点F到平面PCE的距离.
…………………………………(10分)
由已知,PD=有详细的答案或解析.files/image265.gif) ,PF=
,PF=有详细的答案或解析.files/image267.gif) ,PC=
,PC=有详细的答案或解析.files/image269.gif) ,△PFH∽△PCD,∴
,△PFH∽△PCD,∴有详细的答案或解析.files/image271.gif) ,
,
∴FH=有详细的答案或解析.files/image273.gif) .
………………………………………………………………(12分)
.
………………………………………………………………(12分)
解法二:(1)取PC中点M,连结EM,有详细的答案或解析.files/image275.gif)
有详细的答案或解析.files/image012.gif)
有详细的答案或解析.files/image278.gif)
有详细的答案或解析.files/image280.gif)
有详细的答案或解析.files/image282.gif) =
=有详细的答案或解析.files/image284.gif) +
+有详细的答案或解析.files/image012.gif)
有详细的答案或解析.files/image287.gif) =
=有详细的答案或解析.files/image289.gif) ,∴AF∥EM,又EM
,∴AF∥EM,又EM有详细的答案或解析.files/image263.gif) 平面PEC,AF
平面PEC,AF有详细的答案或解析.files/image261.gif) 平面PEC,∴AF∥平面PEC.
………………………………………………(4分)
平面PEC,∴AF∥平面PEC.
………………………………………………(4分)
有详细的答案或解析.files/image293.jpg) (2)以A为坐标原点,分别以
(2)以A为坐标原点,分别以有详细的答案或解析.files/image295.gif) 所在直线为x、y、z
所在直线为x、y、z
轴建立坐标系. ∵PA⊥平面ABCD,CD⊥AD,∴CD⊥PD,
∴∠PDA是二面角P-CD-B的平面角,即∠PDA=45°. ……(6分)
∴A(0, 0, 0), P(0, 0,
2), D(0, 2, 0), F(0, 1, 1), E有详细的答案或解析.files/image297.gif) ,
C(3, 2, 0),设平面PCE的法向量为
,
C(3, 2, 0),设平面PCE的法向量为有详细的答案或解析.files/image299.gif) =(x, y, z),则
=(x, y, z),则有详细的答案或解析.files/image299.gif) ⊥
⊥有详细的答案或解析.files/image302.gif) ,
,有详细的答案或解析.files/image299.gif) ⊥
⊥有详细的答案或解析.files/image304.gif) ,而
,而有详细的答案或解析.files/image302.gif) =(-
=(-有详细的答案或解析.files/image307.gif) ,0,2),
,0,2),
有详细的答案或解析.files/image304.gif) =(
=(有详细的答案或解析.files/image307.gif) ,2,0),∴-
,2,0),∴-有详细的答案或解析.files/image307.gif) x+2z=0,且
x+2z=0,且有详细的答案或解析.files/image307.gif) x+2y=0,解得y=-
x+2y=0,解得y=-有详细的答案或解析.files/image310.gif) x,z=
x,z=有详细的答案或解析.files/image310.gif) x.
取x=4
x.
取x=4
得有详细的答案或解析.files/image299.gif) =(4, -3, 3),………………………………………………………………(10分)
=(4, -3, 3),………………………………………………………………(10分)
又有详细的答案或解析.files/image312.gif) =(0,1,-1),
=(0,1,-1),
故点F到平面PCE的距离为d=有详细的答案或解析.files/image314.gif) .…………(12分)
.…………(12分)
【试题评析】:本小题主要考查直线与平面的位置关系等基本知识,是否利用空间向量供考生选择。考查空间想象能力、逻辑推理能力和运算能力有详细的答案或解析.files/image316.gif)
(二)
17. 解:(1) 设有详细的答案或解析.files/image318.gif) ,则
,则有详细的答案或解析.files/image320.gif) …………………1分
…………………1分
有详细的答案或解析.files/image322.gif) …………………2分
…………………2分
又有详细的答案或解析.files/image002.gif) 是奇函数,所以
是奇函数,所以有详细的答案或解析.files/image325.gif) …………………3分
…………………3分
有详细的答案或解析.files/image327.gif)
有详细的答案或解析.files/image329.gif) =
=有详细的答案或解析.files/image331.gif) ……4分
……4分
………………5分
有详细的答案或解析.files/image002.gif) 是[-1,1]上增函数………………6分
是[-1,1]上增函数………………6分
(2)有详细的答案或解析.files/image333.gif) 是[-1,1]上增函数,由已知得:
是[-1,1]上增函数,由已知得:有详细的答案或解析.files/image335.gif) …………7分
…………7分
等价于有详细的答案或解析.files/image337.gif) …………10分
…………10分
解得:有详细的答案或解析.files/image339.gif) ,所以
,所以有详细的答案或解析.files/image341.gif) …………12分
…………12分
有详细的答案或解析.files/image343.gif)
有详细的答案或解析.files/image345.gif) 二次函数
二次函数有详细的答案或解析.files/image347.gif) 在
在有详细的答案或解析.files/image349.gif) 上递减………………………12分
上递减………………………12分
故有详细的答案或解析.files/image351.gif) 时,
时,有详细的答案或解析.files/image353.gif)
有详细的答案或解析.files/image355.gif) ……………………13分
……………………13分
有详细的答案或解析.files/image357.gif) ,
,有详细的答案或解析.files/image359.gif) …………………………14分
…………………………14分
(三)
16.解: 由题意,得有详细的答案或解析.files/image361.gif) 为锐角,
为锐角,有详细的答案或解析.files/image363.gif) , 3分
, 3分
有详细的答案或解析.files/image365.gif) , 6分
, 6分
由正弦定理得 有详细的答案或解析.files/image367.gif) , 9分
, 9分
有详细的答案或解析.files/image345.gif)
有详细的答案或解析.files/image370.gif) . 12分
. 12分
17.(本题满分12分)
有红蓝两粒质地均匀的正方体形状骰子,红色骰子有两个面是8,四个面是2,蓝色骰子有三个面是7,三个面是1,两人各取一只骰子分别随机掷一次,所得点数较大者获胜.
(1)分别求出两只骰子投掷所得点数的分布列及期望;
(2)求投掷蓝色骰子者获胜的概率是多少?
17.解:(1)设红色骰子投掷所得点数为有详细的答案或解析.files/image372.gif) ,其分布如下:
,其分布如下:
有详细的答案或解析.files/image374.gif)
8
2
P
有详细的答案或解析.files/image092.gif)
|