如图，一无限长光滑斜面的底端静置一个物体，从某时刻开始有一个沿斜面向上的恒力F作用在物体上，使物体沿斜面向上滑去．经过时间t突然撤去该力，又经过相同的时间t物体返回斜面的底部．在物体加速沿斜面上滑的过程中，F的平均功率为

.

P1

，重力的平均功率为

.

P2

．在物体运动的整个过程中，F的瞬时功率的最大值为P₁，重力的瞬时功率的最大值为P₂．则有
（　　）

A． . P1 ： . P2 =4：3	B． . P1 ： . P2 =1：3
C．P1：P2=1：6	D．P1：P2=2：3

查看答案和解析>>

如图，一质量为M=0.4kg的特制玩具小车停在水平轨道上A处，小车前部有一光滑短水平板，平板距离水平轨道竖直高度为h=6cm，平板上静置一质量为m=0.2kg的小球，另一半径为R=47cm的固定半圆轨道CB与水平轨道在同一竖直平面内相接于点B，半圆轨道过B点的切线水平，与小车前部的光滑平板等高．玩具小车在距B点水平距离为L=4.8m处装着小球以恒定功率P₀=8W启动，假设他们水平轨道上受到的阻力恒定，当它们达到最大速度时，小车恰好与半圆轨道在B点相碰，且碰后立即停止，而小球则进入半圆轨道，在B点时其速度V_B=8m/s，即与小车最大速度相同，小球上升到C点时速度水平大小为V_C=4m/s，之后再水平射出又落在水平轨道上的D点．试求：（不计空气阻力，g=10m/s²）
（1）小球最后落到水平轨道上D点时的速度大小；
（2）小球经过半圆轨道过程中，克服摩擦阻力做的功；
（3）小车在水平轨道上加速所用时间．

查看答案和解析>>

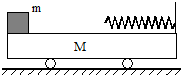如图，质量为M的平板车静止在光滑的水平地面上，小车的左端放一质量为m的木块，车的右端固定一个轻质弹簧，现给木块一个水平向右的瞬时冲量I，木块便沿车板向右滑行，在与弹簧相碰后又沿原路返回，并且恰好能达到小车的左端．试求：
（1）弹簧被压缩到最短时平板小车的动量；
（2）木块返回到小车左端时小车的动能；
（3）弹簧获得最大弹性势能．

查看答案和解析>>

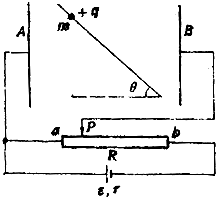如图，质量m、带电+q的小球套在绝缘杆上，杆与水平面成θ角，球杆间摩擦系数为μ，且有μsinθ＞cosθ，杆又放在竖直的平板AB之间，AB间距离为d，并和变阻器及电源相连，变阻器总电阻为R，电源内阻为r．求：
（1）当滑动触头P位于a点时，小球沿杆下滑的加速度为多少？当P由a滑向b时，小球加速度如何变化？
（2）若当P位于变阻器中间时，小球沿杆下滑的加速度恰好达到最大，求这最大加速度值及电源电动势值．

查看答案和解析>>

查看答案和解析>>

一、选择题

1、B    2、C  3、AC    4、D    5、BC  6BC  

7、A  解析：由题意知，地面对物块A的摩擦力为0，对物块B的摩擦力为。

对A、B整体，设共同运动的加速度为a，由牛顿第二定律有：

对B物体，设A对B的作用力为，同理有

联立以上三式得：

 8、B    9、A       10、B

二、实验题

11、⑴ 不变    ⑵ AD  ⑶ABC  ⑷某学生的质量

三、计算题

12、解析：由牛顿第二定律得：mg－f＝ma

    抛物后减速下降有：

                          Δv＝a^/Δt

                    解得：

13、解析：人相对木板奔跑时，设人的质量为，加速度为，木板的质量为M，加速度大小为，人与木板间的摩擦力为，根据牛顿第二定律，对人有：；

（2）设人从木板左端开始距到右端的时间为，对木板受力分析可知：故，方向向左；

由几何关系得：，代入数据得：

（3）当人奔跑至右端时，人的速度，木板的速度；人抱住木柱的过程中，系统所受的合外力远小于相互作用的内力，满足动量守恒条件，有：

　（其中为二者共同速度）

代入数据得，方向与人原来运动方向一致；

以后二者以为初速度向右作减速滑动，其加速度大小为，故木板滑行的距离为。

14. 解析：（1）从图中可以看出，在t＝2s内运动员做匀加速直线运动，其加速度大小为

 =8m/s²

设此过程中运动员受到的阻力大小为f，根据牛顿第二定律，有mg－f＝ma

得           f＝m(g－a)＝80×(10－8)N＝160N

（2）从图中估算得出运动员在14s内下落了

                     39.5×2×2m＝158 m

根据动能定理，有

所以有    ＝（80×10×158－×80×6²）J≈1.25×10⁵J

（3）14s后运动员做匀速运动的时间为

              s＝57s

运动员从飞机上跳下到着地需要的总时间

        t_总＝t＋t′＝（14＋57）s＝71s

15. 13、解析：（1）取竖直向下的方向为正方向。

   球与管第一次碰地前瞬间速度，方向向下。

   碰地的瞬间管的速度，方向向上；球的速度，方向向下，

   球相对于管的速度，方向向下。

   碰后，管受重力及向下的摩擦力，加速度a_管=2g，方向向下，

   球受重力及向上的摩擦力，加速度a_球=3g，方向向上，

球相对管的加速度a_相=5g，方向向上。

取管为参照物，则球与管相对静止前，球相对管下滑的距离为：

要满足球不滑出圆管，则有。

（2）设管从碰地到它弹到最高点所需时间为t₁（设球与管在这段时间内摩擦力方向不变），则：

设管从碰地到与球相对静止所需时间为t₂，

因为t₁ ＞t₂，说明球与管先达到相对静止，再以共同速度上升至最高点，设球与管达到相对静止时离地高度为h’，两者共同速度为v’，分别为：

然后球与管再以共同速度v’作竖直上抛运动，再上升高度h’’为

因此，管上升最大高度H’=h’+h’’=

（3）当球与管第二次共同下落时，离地高为，球位于距管顶处，同题（1）可解得在第二次反弹中发生的相对位移。

16. 解析：(1)小球最后静止在水平地面上，在整个运动过程中，空气阻力做功使其机械能减少，设小球从开始抛出到最后静止所通过的路程S，有 fs=mv₀²/2       已知 f ＝0.6mg    代入算得： s=  5 v₀²/(6g)                

    (2)第一次上升和下降：设上升的加速度为a₁₁．上升所用的时间为t₁₁，上升的最大高度为h₁；下降的加速度为a₁₂，下降所用时间为t₁₂．

    上升阶段：F_合＝mg＋f ＝1.6 mg

    由牛顿第二定律：a₁₁ ＝1.6g           

    根据：v_t＝v₀－a₁₁t₁₁，  v_t＝0

    得：v₀＝l.6gt₁₁， 所以t₁₁＝ 5 v₀/(8g)              

    下降阶段：a₁₂=(mg-f)/m= 0.4g          

    由h₁= a₁₁t₁₁²/2  和 h₂= a₁₂t₁₂²/2      得：t₁₂＝2t₁₁＝5 v₀/(4g)          

    所以上升和下降所用的总时间为：T₁＝t₁₁＋t₁₂＝3t₁₁＝  15 v₀/(8g)        

    第二次上升和下降，以后每次上升的加速度都为a₁₁，下降的加速度都为a₁₂；设上升的初速度为v₂，上升的最大高度为h₂，上升所用时间为t₂₁，下降所用时间为t₂₂

    由v₂²=2a₁₂h₁  和v₀²=2a₁₁h₁          得  v₂＝ v₀/2           

    上升阶段：v₂＝a₁₁t₂₁     得：t₂₁= v₂/ a₁₁=  5 v₀/(16g)       

    下降阶段：  由  h₂= a₁₁t₂₁²/2   和h₂= a₁₂t₂₂²/2        得t₂₂＝2t₂₁       

 所以第二次上升和下降所用总时间为：T₂＝t₂₁＋t₂₂＝3t₂₁＝15 v₀/(16g)= T₁/2    

    第三次上升和下降，设上升的初速度为v₃，上升的最大高度为h₃，上升所用时间为t₃₁，下降所用时间为t₃₂

    由 v₃²=2a₁₁h₂    和v₂²=2a₁₂h₂          得：  v₃＝ v₂/2  = v₀/4

    上升阶段：v₃＝a₁₁t_3l，得t₃₁＝ 5 v₀/(32g)    

    下降阶段：由 h₃= a₁₁t₃₁²/2       和h₃= a₁₂t₃₂²/2            得：t₃₂＝2t₃₁    

    所以第三次上升和下降所用的总时间为：T₃＝t₃₁＋t₃₂＝3t₃₁＝15 v₀/(32g)= T₁/4       

    同理，第n次上升和下降所用的总时间为： T_n＝        

    所以，从抛出到落地所用总时间为： T=15 v₀/(4g)