
题目列表(包括答案和解析)
A.小球落地时动能等于mgH
B.小球陷入泥中的过程中克服泥土阻力所做的功小于刚落到地面时的动能
C.整个过程中小球克服阻力做的功等于mg(H+h)
D.小球在泥土中受到的平均阻力为![]()
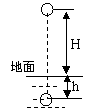
.地面上有一质量为M的重物,用力F向上提它,力F变化而引起物体加速度变化的函数关系如图所示.则关于以下说法中错误的是( )
A、当F小于图中A点值时,物体的重力Mg>F,物体不动
B、图中A点值即为物体的重力值
C、物体向上运动的加速度和力F成正比
D、图线延长和纵轴的交点B的数值等于物体在该地的重力
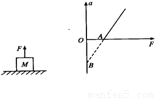
.地面上有一质量为M的重物,用力F向上提它,力F变化而引起物体加速度变化的函数关系如图所示.则关于以下说法中错误的是( )
A、当F小于图中A点值时,物体的重力Mg>F,物体不动
B、图中A点值即为物体的重力值
C、物体向上运动的加速度和力F成正比
D、图线延长和纵轴的交点B的数值等于物体在该地的重力


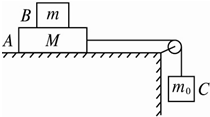 A、B、C三物块质量分别为M、m、m0,作如图所示的连结,绳子不可伸长,且绳子和滑轮的质量、滑轮的摩擦均可不计.若B随A一起沿水平桌面做匀速运动,则( )?
A、B、C三物块质量分别为M、m、m0,作如图所示的连结,绳子不可伸长,且绳子和滑轮的质量、滑轮的摩擦均可不计.若B随A一起沿水平桌面做匀速运动,则( )?一、选择题
1、B 2、C 3、AC 4、D 5、BC 6BC
7、A 解析:由题意知,地面对物块A的摩擦力为0,对物块B的摩擦力为%20牛顿定律在直线运动中的应用.files/image286.gif) 。
。
对A、B整体,设共同运动的加速度为a,由牛顿第二定律有:
%20牛顿定律在直线运动中的应用.files/image288.gif)
对B物体,设A对B的作用力为%20牛顿定律在直线运动中的应用.files/image290.gif) ,同理有
,同理有
%20牛顿定律在直线运动中的应用.files/image292.gif)
联立以上三式得:%20牛顿定律在直线运动中的应用.files/image294.gif)
8、B 9、A 10、B
二、实验题
11、⑴ 不变 ⑵ AD ⑶ABC ⑷某学生的质量
三、计算题
12、解析:由牛顿第二定律得:mg-f=ma
%20牛顿定律在直线运动中的应用.files/image296.gif)
抛物后减速下降有:%20牛顿定律在直线运动中的应用.files/image298.gif)
Δv=a/Δt
解得:%20牛顿定律在直线运动中的应用.files/image300.gif)
13、解析:人相对木板奔跑时,设人的质量为%20牛顿定律在直线运动中的应用.files/image302.gif) ,加速度为
,加速度为%20牛顿定律在直线运动中的应用.files/image304.gif) ,木板的质量为M,加速度大小为
,木板的质量为M,加速度大小为%20牛顿定律在直线运动中的应用.files/image306.gif) ,人与木板间的摩擦力为
,人与木板间的摩擦力为%20牛顿定律在直线运动中的应用.files/image308.gif) ,根据牛顿第二定律,对人有:
,根据牛顿第二定律,对人有:%20牛顿定律在直线运动中的应用.files/image310.gif) ;
;
(2)设人从木板左端开始距到右端的时间为%20牛顿定律在直线运动中的应用.files/image312.gif) ,对木板受力分析可知:
,对木板受力分析可知:%20牛顿定律在直线运动中的应用.files/image314.gif) 故
故%20牛顿定律在直线运动中的应用.files/image316.gif) ,方向向左;
,方向向左;
由几何关系得:%20牛顿定律在直线运动中的应用.files/image318.gif) ,代入数据得:
,代入数据得:%20牛顿定律在直线运动中的应用.files/image320.gif)
(3)当人奔跑至右端时,人的速度%20牛顿定律在直线运动中的应用.files/image322.gif) ,木板的速度
,木板的速度%20牛顿定律在直线运动中的应用.files/image324.gif) ;人抱住木柱的过程中,系统所受的合外力远小于相互作用的内力,满足动量守恒条件,有:
;人抱住木柱的过程中,系统所受的合外力远小于相互作用的内力,满足动量守恒条件,有:
%20牛顿定律在直线运动中的应用.files/image326.gif) (其中
(其中%20牛顿定律在直线运动中的应用.files/image328.gif) 为二者共同速度)
为二者共同速度)
代入数据得%20牛顿定律在直线运动中的应用.files/image330.gif) ,方向与人原来运动方向一致;
,方向与人原来运动方向一致;
以后二者以%20牛顿定律在直线运动中的应用.files/image330.gif) 为初速度向右作减速滑动,其加速度大小为
为初速度向右作减速滑动,其加速度大小为%20牛顿定律在直线运动中的应用.files/image333.gif) ,故木板滑行的距离为
,故木板滑行的距离为%20牛顿定律在直线运动中的应用.files/image335.gif) 。
。
14. 解析:(1)从图中可以看出,在t=2s内运动员做匀加速直线运动,其加速度大小为
%20牛顿定律在直线运动中的应用.files/image337.gif) =
=
设此过程中运动员受到的阻力大小为f,根据牛顿第二定律,有mg-f=ma
得 f=m(g-a)=80×(10-8)N=160N
(2)从图中估算得出运动员在14s内下落了
39.5×2×
根据动能定理,有%20牛顿定律在直线运动中的应用.files/image339.gif)
所以有 %20牛顿定律在直线运动中的应用.files/image341.gif) =(80×10×158-
=(80×10×158-%20牛顿定律在直线运动中的应用.files/image343.gif) ×80×62)J≈1.25×105J
×80×62)J≈1.25×105J
(3)14s后运动员做匀速运动的时间为
%20牛顿定律在直线运动中的应用.files/image345.gif) s=57s
s=57s
运动员从飞机上跳下到着地需要的总时间
t总=t+t′=(14+57)s=71s
15. 13、解析:(1)取竖直向下的方向为正方向。
球与管第一次碰地前瞬间速度%20牛顿定律在直线运动中的应用.files/image347.gif) ,方向向下。
,方向向下。
碰地的瞬间管的速度%20牛顿定律在直线运动中的应用.files/image349.gif) ,方向向上;球的速度
,方向向上;球的速度%20牛顿定律在直线运动中的应用.files/image351.gif) ,方向向下,
,方向向下,
球相对于管的速度%20牛顿定律在直线运动中的应用.files/image353.gif) ,方向向下。
,方向向下。
碰后,管受重力及向下的摩擦力,加速度a管=
球受重力及向上的摩擦力,加速度a球=
球相对管的加速度a相=
取管为参照物,则球与管相对静止前,球相对管下滑的距离为:
%20牛顿定律在直线运动中的应用.files/image355.gif)
要满足球不滑出圆管,则有%20牛顿定律在直线运动中的应用.files/image357.gif) 。
。
(2)设管从碰地到它弹到最高点所需时间为t1(设球与管在这段时间内摩擦力方向不变),则:%20牛顿定律在直线运动中的应用.files/image359.gif)
设管从碰地到与球相对静止所需时间为t2,%20牛顿定律在直线运动中的应用.files/image361.gif)
因为t1 >t2,说明球与管先达到相对静止,再以共同速度上升至最高点,设球与管达到相对静止时离地高度为h’,两者共同速度为v’,分别为:
%20牛顿定律在直线运动中的应用.files/image363.gif)
%20牛顿定律在直线运动中的应用.files/image365.gif)
然后球与管再以共同速度v’作竖直上抛运动,再上升高度h’’为
%20牛顿定律在直线运动中的应用.files/image367.gif)
因此,管上升最大高度H’=h’+h’’=%20牛顿定律在直线运动中的应用.files/image369.gif)
(3)当球与管第二次共同下落时,离地高为%20牛顿定律在直线运动中的应用.files/image369.gif) ,球位于距管顶
,球位于距管顶%20牛顿定律在直线运动中的应用.files/image371.gif) 处,同题(1)可解得在第二次反弹中发生的相对位移。
处,同题(1)可解得在第二次反弹中发生的相对位移。
16. 解析:(1)小球最后静止在水平地面上,在整个运动过程中,空气阻力做功使其机械能减少,设小球从开始抛出到最后静止所通过的路程S,有 fs=mv02/2 已知 f =0.6mg 代入算得: s= 5
v02/(
(2)第一次上升和下降:设上升的加速度为a11.上升所用的时间为t11,上升的最大高度为h1;下降的加速度为a12,下降所用时间为t12.
上升阶段:F合=mg+f =1.6 mg
由牛顿第二定律:a11 =
根据:vt=v0-a11t11, vt=0
得:v0=l.6gt11, 所以t11= 5 v0/(
下降阶段:a12=(mg-f)/m=
由h1= a11t112/2 和 h2= a12t122/2 得:t12=2t11=5 v0/(
所以上升和下降所用的总时间为:T1=t11+t12=3t11= 15 v0/(
第二次上升和下降,以后每次上升的加速度都为a11,下降的加速度都为a12;设上升的初速度为v2,上升的最大高度为h2,上升所用时间为t21,下降所用时间为t22
由v22=
上升阶段:v2=a11t21 得:t21= v2/
a11= 5 v0/(
下降阶段: 由 h2= a11t212/2 和h2= a12t222/2 得t22=2t21
所以第二次上升和下降所用总时间为:T2=t21+t22=3t21=15 v0/(
第三次上升和下降,设上升的初速度为v3,上升的最大高度为h3,上升所用时间为t31,下降所用时间为t32
由 v32=
上升阶段:v3=a11t
下降阶段:由 h3= a11t312/2 和h3= a12t322/2 得:t32=2t31
所以第三次上升和下降所用的总时间为:T3=t31+t32=3t31=15 v0/(
同理,第n次上升和下降所用的总时间为: Tn=%20牛顿定律在直线运动中的应用.files/image373.gif)
所以,从抛出到落地所用总时间为: T=15 v0/(
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com