
题目列表(包括答案和解析)
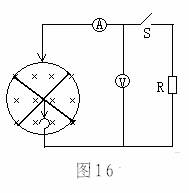 在磁感应强度为B=0.4 T的匀强磁场中放一个半径r0=50 cm的圆形导轨,上面搁有互相垂直的两根导体棒,一起以角速度ω=103 rad/s逆时针匀速转动。圆导轨边缘和两棒中央通过电刷与外电路连接,若每根导体棒的有效电阻为R0=0.8
Ω,外接电阻R=3.9 Ω,如图16所示,求:
在磁感应强度为B=0.4 T的匀强磁场中放一个半径r0=50 cm的圆形导轨,上面搁有互相垂直的两根导体棒,一起以角速度ω=103 rad/s逆时针匀速转动。圆导轨边缘和两棒中央通过电刷与外电路连接,若每根导体棒的有效电阻为R0=0.8
Ω,外接电阻R=3.9 Ω,如图16所示,求:
(1)每半根导体棒产生的感应电动;
(2)当电键S接通和断开时两电表示数(电压表和电流表为理想电表).
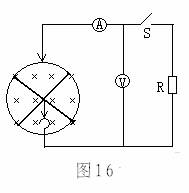 在磁感应强度为B=0.4 T的匀强磁场中放一个半径r0=50 cm的圆形导轨,上面搁有互相垂直的两根导体棒,一起以角速度ω=103 rad/s逆时针匀速转动。圆导轨边缘和两棒中央通过电刷与外电路连接,若每根导体棒的有效电阻为R0=0.8Ω,外接电阻R=3.9 Ω,如图16所示,求:
在磁感应强度为B=0.4 T的匀强磁场中放一个半径r0=50 cm的圆形导轨,上面搁有互相垂直的两根导体棒,一起以角速度ω=103 rad/s逆时针匀速转动。圆导轨边缘和两棒中央通过电刷与外电路连接,若每根导体棒的有效电阻为R0=0.8Ω,外接电阻R=3.9 Ω,如图16所示,求:
(1)每半根导体棒产生的感应电动;
(2)当电键S接通和断开时两电表示数(电压表和电流表为理想电表).
(1)质子进入磁场中的速度;
(2)质子在磁场中运动的轨道半径;
(3)质子做匀速圆周运动的周期.
一个初速度为零的质子,经过电压为1.30×103 V的电场加速后,垂直进入磁感应强度为B=0.20 T的匀强磁场(质子质量m=1.67×10-27 kg,电荷量q=1.6×10-19 C).试求:
(1)质子进入磁场中的速度;
(2)质子在磁场中运动的轨道半径;
(3)质子做匀速圆周运动的周期.
图
1. C 2. B 3. C 4. ABC 5. AC
6. AD 7. C 8. AB 9. D 10. A
11. 0.63
12. 镇流器的自感现象 断开瞬间 只有在电路刚断开时才能产生很高的自感电动势使人产生触电的感觉
13. Br2ω/2 ,0
14. 解:(1)由题意知,带电粒子从C孔进入,与筒壁碰撞两次再从C孔射出经历的时间为最短,由%20电磁学与电磁感应综合.files/image232.gif) ,粒子由C孔进入磁场,在磁场中做匀速圆周运动的速度
,粒子由C孔进入磁场,在磁场中做匀速圆周运动的速度%20电磁学与电磁感应综合.files/image234.gif) ,由
,由%20电磁学与电磁感应综合.files/image236.gif) ,即
,即%20电磁学与电磁感应综合.files/image238.gif) ,得
,得%20电磁学与电磁感应综合.files/image240.gif)
(2)粒子从%20电磁学与电磁感应综合.files/image242.gif) 的加速度为
的加速度为%20电磁学与电磁感应综合.files/image244.gif) ,
,%20电磁学与电磁感应综合.files/image246.gif) ,粒子从
,粒子从%20电磁学与电磁感应综合.files/image242.gif) 的时间为
的时间为%20电磁学与电磁感应综合.files/image249.gif) ;粒子在磁场中运动的时间为
;粒子在磁场中运动的时间为%20电磁学与电磁感应综合.files/image251.gif) ,将(1)求得的B值代入,得
,将(1)求得的B值代入,得%20电磁学与电磁感应综合.files/image253.gif) ,求得
,求得%20电磁学与电磁感应综合.files/image255.gif)
15. 解:(1)感应电动势的最大值:%20电磁学与电磁感应综合.files/image257.gif)
(2)由欧姆定律得电流的最大值:%20电磁学与电磁感应综合.files/image259.gif) =0.16A
=0.16A
电流的有效值%20电磁学与电磁感应综合.files/image261.gif) =0.11A
=0.11A
(3)用电器上消耗的电功率:%20电磁学与电磁感应综合.files/image263.gif)
16. 解:(1)ab脱离EF前,电路中的磁通量的变化为
%20电磁学与电磁感应综合.files/image265.gif)
平均感应电动势为%20电磁学与电磁感应综合.files/image267.gif) ,
,
有%20电磁学与电磁感应综合.files/image269.gif)
(2)ab脱离EF时,回路中通过电流最大,即%20电磁学与电磁感应综合.files/image271.gif) ,
,
ab脱离EF后,电路中不在有电流,并且ab倒下过程中只有小球的重力做功,机械能守恒,即%20电磁学与电磁感应综合.files/image273.gif)
ab上各处切割磁感线的速度是不同的,其等效切割速度应等于ab中点的速度
%20电磁学与电磁感应综合.files/image275.gif)
联立解得%20电磁学与电磁感应综合.files/image277.gif)
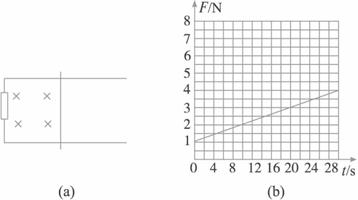
17.解:(1)经过时间%20电磁学与电磁感应综合.files/image279.gif) 后,MN运动的距离为
后,MN运动的距离为%20电磁学与电磁感应综合.files/image281.gif) ,由图可知直导线MN在闭合回路中的有效长度为
,由图可知直导线MN在闭合回路中的有效长度为%20电磁学与电磁感应综合.files/image283.gif) ,
,
此时感应电动势的瞬时值:%20电磁学与电磁感应综合.files/image285.gif) (V)
(V)
(2)此时闭合回路中的总长度为:%20电磁学与电磁感应综合.files/image287.gif)
%20电磁学与电磁感应综合.files/image289.gif)
闭合回路中的总电阻:%20电磁学与电磁感应综合.files/image291.gif)
%20电磁学与电磁感应综合.files/image293.gif)
根据全电路的欧姆定律,电流大小:%20电磁学与电磁感应综合.files/image295.gif) (A),由右手定律可得电流方向在闭合回路中是逆时针方向
(A),由右手定律可得电流方向在闭合回路中是逆时针方向
(3)此时MN中不在闭合回路中的导线MP的长度为%20电磁学与电磁感应综合.files/image297.gif)
产生的电动势%20电磁学与电磁感应综合.files/image299.gif) (V)
(V)
在闭合回路中的导线PN两端电压%20电磁学与电磁感应综合.files/image301.gif) (V)
(V)
所以MN两端的电压%20电磁学与电磁感应综合.files/image230.gif)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com