
题目列表(包括答案和解析)
|
| 1 |
| 2 |
(本题满分12分)已知![]()
(1)若函数![]() 的定义域为
的定义域为![]() ;当
;当![]() 时,求
时,求![]() 的最大值和最小值。
的最大值和最小值。
(2)要使![]() 对
对![]() 恒成立,求
恒成立,求![]() 的取值范围。
的取值范围。
(本小题满分12分)设二次函数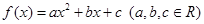 满足下列条件:
满足下列条件:
①当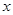 ∈R时,
∈R时,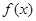 的最小值为0,且f (
的最小值为0,且f (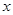 -1)=f(-
-1)=f(-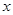 -1)成立;
-1)成立;
②当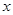 ∈(0,5)时,
∈(0,5)时,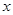 ≤
≤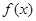 ≤2
≤2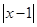 +1恒成立。
+1恒成立。
(1)求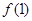 的值;
的值;
(2)求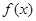 的解析式;
的解析式;
(3)求最大的实数m(m>1),使得存在实数t,只要当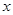 ∈
∈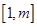 时,就有
时,就有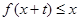 成立。
成立。
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| k2 |
| 4 |
| 1 |
| 2 |
一、选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有 一项是符合题目要求的。
题号
1
2
3
4
5
6
7
8
9
10
答案
二、填空题:(本大题共5个小题,每小题5分,共25分,)
11. 12. 13. 14. 15.
三、解答题:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com