
题目列表(包括答案和解析)
(本小题满分14分)某地区的农产品 第
第 天
天 的销售价格
的销售价格 (元∕百斤),一农户在第
(元∕百斤),一农户在第 天
天 农产品
农产品 的销售量
的销售量 (百斤)。
(百斤)。
(1)求该农户在第7天销售农产品 的收入;
的收入;
(2)问这20天中该农户在哪一天的销售收入最大?
(本小题满分14分)某公司决定采用增加广告投入和技术改造投入两项措施来获得更大的收益.通过对市场的预测,当对两项投入都不大于3(百万元)时,每投入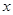 (百万元)广告费,增加的销售额可近似的用函数
(百万元)广告费,增加的销售额可近似的用函数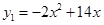 (百万元)来计算;每投入x(百万元)技术改造费用,增加的销售额可近似的用函数
(百万元)来计算;每投入x(百万元)技术改造费用,增加的销售额可近似的用函数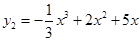 (百万元)来计算.现该公司准备共投入3(百万元),分别用于广告投入和技术改造投入,请设计一种资金分配方案,使得该公司的销售额最大. (参考数据:≈1.41,≈1.73)
(百万元)来计算.现该公司准备共投入3(百万元),分别用于广告投入和技术改造投入,请设计一种资金分配方案,使得该公司的销售额最大. (参考数据:≈1.41,≈1.73)
(本小题满分14分)
某家具厂有方木料90m3,五合板600m2,准备加工成书桌和书橱出售.已知生产每张书桌需要方木料0.1m3,五合板2m2,生产每个书橱需要方木料0.2m2,五合板1m2,出售一张方桌可获利润80元,出售一个书橱可获利润120元.
(1)如果只安排生产书桌,可获利润多少?
(2)怎样安排生产可使所得利润最大?
.(本小题满分14分)

某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段 ,
, …
… 后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
(1)求第四小组的频率,并补全这个频率分布直方图;
(2)估计这次考试的及格率(60分及以上为及格)和平均分;
(3)用分层抽样的方法从成绩是80分以上(包括80分)的学生中抽取了6人进行试卷分析,再从这6个人中选2人作学习经验介绍发言,求选出的2人中至少有1人在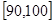 的概率.
的概率.
(本小题满分14分)
某光学仪器厂有一条价值为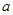 万元的激光器生产线,计划通过技术改造来提高该生产线的生产能力,提高产品的增加值. 经过市场调查,产品的增加值
万元的激光器生产线,计划通过技术改造来提高该生产线的生产能力,提高产品的增加值. 经过市场调查,产品的增加值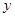 万元与技术改造投入
万元与技术改造投入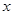 万元之间满足:①
万元之间满足:①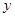 与
与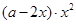 成正比;②当
成正比;②当 时,
时,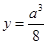 ,并且技术改造投入满足
,并且技术改造投入满足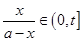 ,其中
,其中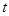 为常数且
为常数且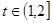 .
.
(I)求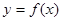 表达式及定义域;
表达式及定义域;
(II)求技术改造之后,产品增加值的最大值及相应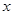 的值.
的值.
第Ⅰ卷
一、填空题:
1. {1,2,3}; 2.充分非必要;3. ; 4.
; 4. ; 5. 8; 6. (历史) 5049; (物理)
; 5. 8; 6. (历史) 5049; (物理)  ; 7. 1; 8.
; 7. 1; 8.
9. ;10.
;10. ; 11.
; 11. ; 12.
; 12. ;13.
;13.
 ;14. 4.
;14. 4.
二、解答题:
15. 解:(1)因为 ,所以
,所以 …………(3分)
…………(3分)
得 (用辅助角得到
(用辅助角得到 同样给分) ………(5分)
同样给分) ………(5分)
又 ,所以
,所以 =
= ……………………………………(7分)
……………………………………(7分)
(2)因为 ………………………(9分)
………………………(9分)
= …………………………………………(11分)
…………………………………………(11分)
所以当 =
= 时,
时,  的最大值为5+4=9 …………………(13分)
的最大值为5+4=9 …………………(13分)
故 的最大值为3 ………………………………………(14分)
的最大值为3 ………………………………………(14分)
16. (选历史方向) 解: (1)表格为:
高 个
非高个
合 计
大 脚
5
2
7
非大脚
1
13
合 计
6
14
…… (3分)
(说明:黑框内的三个数据每个1分,黑框外合计数据有错误的暂不扣分)
(2)提出假设H0: 人的脚的大小与身高之间没有关系. …………………………… (4分)
根据上述列联表可以求得 .…………………… (7分)
.…………………… (7分)
当H0成立时, 的概率约为0.005,而这里8.802>7.879,
的概率约为0.005,而这里8.802>7.879,
所以我们有99.5%的把握认为: 人的脚的大小与身高之间有关系. ……………… (8分)
(3)
①抽到12号的概率为 ………………………………… (11分)
………………………………… (11分)
②抽到“无效序号(超过20号)”的概率为 …………………… (14分)
…………………… (14分)
(选物理方向) 解:(Ⅰ)在给定的直角坐标系下,设最高点为A,入水点为B,
抛物线的解析式为 . …………………………… 2′
. …………………………… 2′
由题意,知O(0,0),B(2,-10),且顶点A的纵坐标为 .…………… 4′
.…………… 4′
 或
或 ……………………………
8′
……………………………
8′
∵抛物线对称轴在y轴右侧,∴ ,又∵抛物线开口向下,∴a<0,
,又∵抛物线开口向下,∴a<0,
从而b>0,故有 ……………………………9′
……………………………9′
∴抛物线的解析式为 . ……………………………10′
. ……………………………10′
(Ⅱ)当运动员在空中距池边的水平距离为 米时,
米时,
即 时,
时, , ……………………………12′
, ……………………………12′
∴此时运动员距水面的高为10- =
= <5,因此,此次跳水会失误.………………14′
<5,因此,此次跳水会失误.………………14′
17. (1)证明:由直四棱柱,得 ,
,
所以 是平行四边形,所以
是平行四边形,所以 …………………(3分)
…………………(3分)
而 ,
, ,所以
,所以 面
面 ………(4分)
………(4分)
(2)证明:因为 , 所以
, 所以 ……(6分)
……(6分)
又因为 ,且
,且 ,所以
,所以 ………
……(8分)
………
……(8分)
而 ,所以
,所以 …………………………(9分)
…………………………(9分)
(3)当点 为棱
为棱 的中点时,平面
的中点时,平面
 平面
平面 …………………(10分)
…………………(10分)
 取DC的中点N,
取DC的中点N, ,连结
,连结 交
交 于
于 ,连结
,连结 .
.
因为N是DC中点,BD=BC,所以 ;又因为DC是面ABCD与面
;又因为DC是面ABCD与面 的交线,而面ABCD⊥面
的交线,而面ABCD⊥面 ,
,
所以 ……………(12分)
……………(12分)
又可证得, 是
是 的中点,所以BM∥ON且BM=ON,即BMON是平行四边形,所以BN∥OM,所以OM
的中点,所以BM∥ON且BM=ON,即BMON是平行四边形,所以BN∥OM,所以OM 平面
平面 ,
,
因为OM?面DMC1,所以平面
 平面
平面 ………………………(14分)
………………………(14分)
18. 解:(1)因为 ,所以c=1……………………(2分)
,所以c=1……………………(2分)
则b=1,即椭圆 的标准方程为
的标准方程为 …………………………(4分)
…………………………(4分)
(2)因为 (1,1),所以
(1,1),所以 ,所以
,所以 ,所以直线OQ的方程为y=-2x(6分)
,所以直线OQ的方程为y=-2x(6分)
又椭圆的左准线方程为x=-2,所以点Q(-2,4) …………………………(7分)
所以 ,又
,又 ,所以
,所以 ,即
,即 ,
,
故直线 与圆
与圆 相切……………………………………………………(9分)
相切……………………………………………………(9分)
(3)当点 在圆
在圆 上运动时,直线
上运动时,直线 与圆
与圆 保持相切 ………(10分)
保持相切 ………(10分)
证明:设 (
( ),则
),则 ,所以
,所以 ,
, ,
,
所以直线OQ的方程为 ……………(12分)
……………(12分)
所以点Q(-2, ) ………………
(13分)
) ………………
(13分)
所以 ,
,
又 ,所以
,所以 ,即
,即 ,故直线
,故直线 始终与圆
始终与圆 相切……(15分)
相切……(15分)
19.⑴解:函数的定义域为 ,
, (
( )…… (2分)
)…… (2分)
若 ,则
,则 ,
, 有单调递增区间
有单调递增区间 . ……………… (3分)
. ……………… (3分)
若 ,令
,令 ,得
,得 ,
,
当 时,
时, ,
,
当 时,
时, . ……………… (5分)
. ……………… (5分)
 有单调递减区间
有单调递减区间 ,单调递增区间
,单调递增区间 . ……………… (6分)
. ……………… (6分)
⑵解:(i)若 ,
, 在
在 上单调递增,所以
上单调递增,所以 . ……… (7分)
. ……… (7分)
若 ,
, 在
在 上单调递减,在
上单调递减,在 上单调递增,
上单调递增,
所以 . ………………
(9分)
. ………………
(9分)
若 ,
, 在
在 上单调递减,所以
上单调递减,所以 .………… (10分)
.………… (10分)
综上所述, ……………… (12分)
……………… (12分)
(ii)令 .若
.若 ,无解. ………………
(13分)
,无解. ………………
(13分)
若 ,解得
,解得 . ……………… (14分)
. ……………… (14分)
若 ,解得
,解得 . ………………
(15分)
. ………………
(15分)
故 的取值范围为
的取值范围为 . ……………… (16分)
. ……………… (16分)
20. (1)数表中第 行的数依次所组成数列的通项为
行的数依次所组成数列的通项为 ,则由题意可得
,则由题意可得
 … (2分)
… (2分)

 (其中
(其中 为第
为第 行数所组成的数列的公差)
(4分)
行数所组成的数列的公差)
(4分)
(2)
 第一行的数依次成等差数列,由(1)知,第2行的数也依次成等差数列,依次类推,可知数表中任一行的数(不少于3个)都依次成等差数列. ……………… (5分)
第一行的数依次成等差数列,由(1)知,第2行的数也依次成等差数列,依次类推,可知数表中任一行的数(不少于3个)都依次成等差数列. ……………… (5分)
设第 行的数公差为
行的数公差为 ,则
,则 ,则
,则 …………… (6分)
…………… (6分)
所以




 (10 分)
(10 分)
(3)由 ,可得
,可得
所以
 =
= ……………… (11分)
……………… (11分)
令 ,则
,则 ,所以
,所以 
 ………… (13分)
………… (13分)
要使得 ,即
,即 ,只要
,只要 =
= ,
,
 ,
, ,所以只要
,所以只要 ,
,
即只要 ,所以可以令
,所以可以令
则当 时,都有
时,都有 .
.
所以适合题设的一个函数为 (16分)
(16分)
第Ⅱ卷(附加题 共40分)
1. (1)设动点P的坐标为 ,M的坐标为
,M的坐标为 ,
,
则 即为所求的轨迹方程. …………(6分)
即为所求的轨迹方程. …………(6分)
(2)由(1)知P的轨迹是以( )为圆心,半径为
)为圆心,半径为 的圆,易得RP的最小值为1
的圆,易得RP的最小值为1
.……(10分)
2.  ,|x-a|<l,
,|x-a|<l,


 ,
…………………………………………………5分
,
…………………………………………………5分
=

 ………………………10分
………………………10分
3. 证明:以 为坐标原点
为坐标原点 长为单位长度,如图建立空间直角坐标系,则各点坐标为
长为单位长度,如图建立空间直角坐标系,则各点坐标为
 .
.
(1)解:因

所以, 与
与 所成的角余弦值为
所成的角余弦值为 …………………………………5分
…………………………………5分
(2)解:在 上取一点
上取一点 ,则存在
,则存在 使
使

要使

 为
为
所求二面角 的平面角.
的平面角.


 …………………………………10分
…………………………………10分
另解:可以计算两个平面的法向量分别为:平面AMC的法向量 ,平面BMC的法向量为
,平面BMC的法向量为 ,
, =
= , 所求二面角
, 所求二面角 的余弦值为-
的余弦值为- .
.
4. (1)记事件A为“任取两张卡片,将卡片上的函数相加得到的函数是奇函数”,由题意知 ………………………………4分
………………………………4分
(2)ξ可取1,2,3,4.
 ,
,
 ;………………8分
;………………8分
故ξ的分布列为
ξ
1
2
3
4
P





答:ξ的数学期望为 ………………………………10分
………………………………10分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com