
题目列表(包括答案和解析)
 ,x∈[0,+∞),若f(x)图象上的点都位于直线y=
,x∈[0,+∞),若f(x)图象上的点都位于直线y=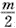 +x+
+x+ 的上方,求实数m的取值范围。
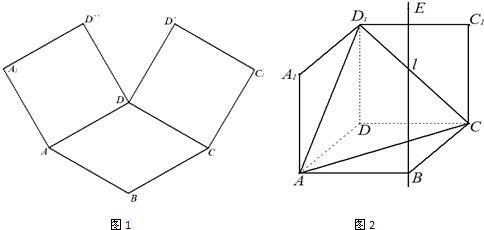
的上方,求实数m的取值范围。| D1E |
 所成的比λ;若不存在,请说明理由.
所成的比λ;若不存在,请说明理由.
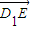 所成的比λ;若不存在,请说明理由.
所成的比λ;若不存在,请说明理由.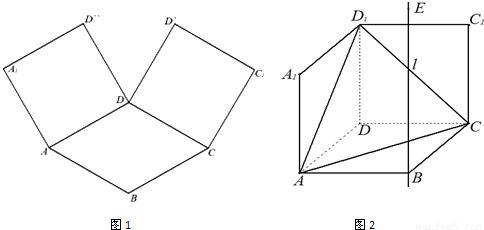
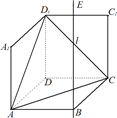 如图1,在平面内,ABCD是∠BAD=60°,且AB=a的菱形,ADD′′A1和CD D′C1都是正方形.将两个正方形分别沿AD,CD折起,使D′′与D′重合于点D1.设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧(图2).
如图1,在平面内,ABCD是∠BAD=60°,且AB=a的菱形,ADD′′A1和CD D′C1都是正方形.将两个正方形分别沿AD,CD折起,使D′′与D′重合于点D1.设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧(图2).| π |
| 4 |
| π |
| 3 |
| D1P |
| PE |
| D1P |
| PE |
1.--数学.files/image101.gif) 2.
2.--数学.files/image103.gif) 3.
3.--数学.files/image105.gif) 4.甲
5.
4.甲
5.--数学.files/image107.gif)
6.--数学.files/image109.gif) 7.
7.--数学.files/image111.gif) 8.
8.--数学.files/image113.gif) 9.
9.--数学.files/image115.gif) 10.
10.--数学.files/image117.gif) 11.
11.--数学.files/image119.gif) 12.
12.--数学.files/image121.gif)
13. (1)直三棱柱ABC―A1B
则BB1⊥AB,BB1⊥BC,
又由于AC=BC=BB1=1,AB1=--数学.files/image123.gif) ,则AB=
,则AB=--数学.files/image125.gif) ,
,
则由AC2+BC2=AB2可知,AC⊥BC,
又由上BB1⊥底面ABC可知BB1⊥AC,则AC⊥平面B1CB,
所以有平面AB
(2)三棱锥A1―AB--数学.files/image127.gif) .----------14分
.----------14分
(注:还有其它转换方法)
14. 解:(1)由条件知 --数学.files/image129.gif) 恒成立
恒成立
又∵取x=2时,--数学.files/image131.gif) 与恒成立, ∴
与恒成立, ∴--数学.files/image089.gif) .
.
(2)∵--数学.files/image134.gif) ∴
∴--数学.files/image136.gif) ∴
∴--数学.files/image138.gif) .
.
又 --数学.files/image083.gif) 恒成立,即
恒成立,即--数学.files/image141.gif) 恒成立.
恒成立.
∴--数学.files/image143.gif) ,
,
解出:--数学.files/image145.gif) ,
,
∴--数学.files/image147.gif) .
.
(3)由分析条件知道,只要--数学.files/image149.gif) 图象(在y轴右侧)总在直线
图象(在y轴右侧)总在直线 --数学.files/image151.gif) 上方即可,也就是直线的斜率
上方即可,也就是直线的斜率--数学.files/image153.gif) 小于直线与抛物线相切时的斜率位置,于是:
小于直线与抛物线相切时的斜率位置,于是:
--数学.files/image155.gif)
∴--数学.files/image157.gif) .
.
解法2:--数学.files/image159.gif) 必须恒成立,
必须恒成立,
即 --数学.files/image161.gif) 恒成立.
恒成立.
①△<0,即 [4(1-m)]2-8<0,解得:--数学.files/image163.gif) ;
;
②--数学.files/image165.gif) 解出:
解出:--数学.files/image167.gif) .
.
总之,--数学.files/image157.gif) .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com