题目列表(包括答案和解析)
（本小题满分10分）（注意：在试题卷上作答无效）
在△
中，角
、
、
所对的边分别为
、
、
，且
.
（Ⅰ）若
，求角；
w ww.ks 5u.c om
（Ⅱ）设
，
，试求
的最大值.
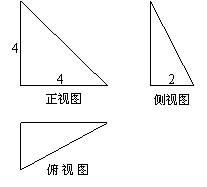
一个三棱w ww.ks 5u.c om锥的三视图是三个直角三角形，如图所示，在包围该三棱锥的外接球内任取一点，该点落在三棱锥内部的概率为（ ）
A. 
B. 
C. 
D. 
 |
已知l1和l2是平面内互相垂直的两条直线，它们的交点为A，动点B、C分别在l1和l2
上，且
，过A、B、C三点的动圆所形成的区域的面积为 .
w ww.ks 5u.co m
已知l1和l2是平面内互相垂直的两条直线，它们的交点为A，动点B、C分别在l1和l2
上，且
，过A、B、C三点的动圆所形成的区域的面积为 .
w ww.ks 5u.co m
（本题满分16分）如图，已知椭圆
：
的长轴
长为4，离心率
，
为坐标原点，过
的直线
与
轴垂直．
是椭圆上异于
、的任意一点，
轴，
为垂足，延长
到点
使得
，连结
延长交直线于点
，
为
的中点．
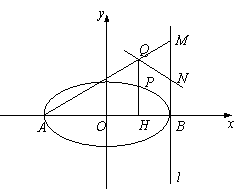（1）求椭圆的方程；w ww.ks 5u.co m
（2）证明点在以为直径的圆上；
（3）试判断直线
与圆的位置关系．
一、填空题：
1、
2、
3、对任意
使
4、2 5、
6、
7、
8、8
9、
10、40
11、
12、4
13、解：（1）解：
，
由
，有
，
解得
。
……7分
（2）解法一：
……11分
。 ……15分
解法二：由（1），，得
∴
∴
……10分
于是
，
……12分
代入得
。
……15分
14、（1）解：①若直线
的斜率不存在，即直线是
，符合题意。 ……2分
②若直线斜率存在，设直线为
，即
。
由题意知，圆心
以已知直线的距离等于半径2，即：
，
解之得
……5分
所求直线方程是，
……6分
（2）解法一：直线与圆相交，斜率必定存在，且不为0，可设直线方程为
由
得
……8分
又直线
与垂直，由
得
……11分
∴
……13分
为定值。
故
是定值，且为6。
……15分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com