
题目列表(包括答案和解析)
(本小题满分13分)某购物广场拟在五一节举行抽奖活动,规则是:从装有编号为0,1,2,3四个小球的抽奖箱中同时抽出两个小球,两个小球号码相加之和等于5中一等奖,等于4中二等奖,等于3中三等奖.
(1)求中三等奖的概率;
(2)求中奖的概率.
(本小题满分12分)
设函数 是定义域在
是定义域在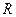 ,并且满足
,并且满足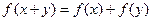 ,
,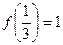 ,且当
,且当 >0时,
>0时,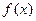 <0。
<0。
(1)求 的值,
的值,
(2)判断函数的奇偶性,
(3)如果 ,求
,求 的取值范围。
的取值范围。
(本小题满分12分)
如图甲,在平面四边形ABCD中,已知
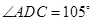 ,
,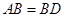 ,现将四边形ABCD沿BD折起,使平面ABD
,现将四边形ABCD沿BD折起,使平面ABD 平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.
平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.

(1)求证:DC 平面ABC;
平面ABC;
(2)设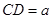 ,求三棱锥A-BFE的体积.
,求三棱锥A-BFE的体积.
(本小题满分12分)(1)对于定义在 上的函数
上的函数 ,满足
,满足 ,求证:函数
,求证:函数 在
在 上是减函数;
上是减函数;
(2)请你认真研读(1)中命题并联系以下命题:若 是定义在
是定义在 上的可导函数,满足
上的可导函数,满足 ,则
,则 是
是 上的减函数。然后填空建立一个普遍化的命题
上的减函数。然后填空建立一个普遍化的命题 :
:
设 是定义在
是定义在 上的可导函数,
上的可导函数, ,若
,若  +
+
 ,
,
则 是 上的减函数。
上的减函数。
注:命题的普遍化就是从考虑一个对象过渡到考虑包含该对象的一个集合;或者从考虑一个较小的集合过渡到考虑包含该较小集合的更大集合。
(3)证明(2)中建立的普遍化命题。
(本小题满分12分)
如图1,在平面内,ABCD边长为2的正方形,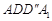 和
和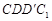 都是正方形。将两个正方形分别沿AD,CD折起,使
都是正方形。将两个正方形分别沿AD,CD折起,使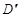 与
与 重合于点D1。设直线l过点B且垂直于正方形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧,设
重合于点D1。设直线l过点B且垂直于正方形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧,设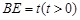 (图2)。
(图2)。
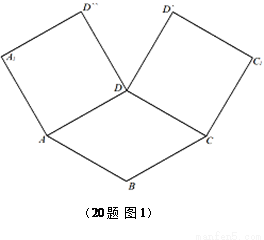
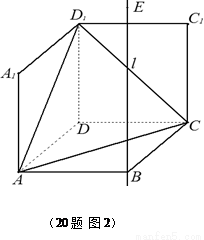
(1)设二面角E – AC – D1的大小为q ,当 时,求
时,求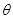 的余弦值;
的余弦值;
(2)当 时在线段
时在线段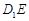 上是否存在点
上是否存在点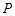 ,使平面
,使平面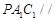 平面
平面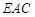 ,若存在,求出
,若存在,求出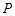 分
分 所成的比
所成的比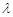 ;若不存在,请说明理由。
;若不存在,请说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com