
题目列表(包括答案和解析)
(文)某电信部门执行的新的电话收费标准中,其中本地网营业区内的通话费标准:前3分钟为0.20元(不足3分钟按3分钟计算),以后的每分钟收0.10元(不足1分钟按1分钟计算。)在一次实习作业中,某同学调查了A、B、C、D、E五人某天拨打的本地网营业区内的电话通话时间情况,其原始数据如下表所示:
|
|
A |
B |
C |
D |
E |
|
第一次通话时间 |
3分 |
3分45秒 |
3分55秒 |
3分20秒 |
6分 |
|
第二次通话时间 |
0分 |
4分 |
3分40秒 |
4分50秒 |
0分 |
|
第三次通话时间 |
0分 |
0分 |
5分 |
2分 |
0分 |
|
应缴话费(元) |
|
|
|
|
|
(1)在上表中填写出各人应缴的话费;
(2)设通话时间为t分钟,试根据上表完成下表的填写(即这五人在这一天内的通话情况统计表):
|
时间段 |
频数累计 |
频数 |
频率 |
累计频率 |
|
0<t≤3 |
┯ |
2 |
0.2 |
0.2 |
|
3<t≤4 |
|
|
|
|
|
4<t≤5 |
|
|
|
|
|
5<t≤6 |
|
|
|
|
|
合计 |
正 正 |
|
|
|
(3)若该本地网营业区原来执行的电话收费标准是:每3分钟为0.20元(不足3分钟按3分钟计算)。问这五人这天的实际平均通话费与原通话标准下算出的平均通话费相比,是增多了还是减少了?增或减了多少?
(文)某电信部门执行的新的电话收费标准中,其中本地网营业区内的通话费标准:前3分钟为0.20元(不足3分钟按3分钟计算),以后的每分钟收0.10元(不足1分钟按1分钟计算。)在一次实习作业中,某同学调查了A、B、C、D、E五人某天拨打的本地网营业区内的电话通话时间情况,其原始数据如下表所示:
| | A | B | C | D | E |
| 第一次通话时间 | 3分 | 3分45秒 | 3分55秒 | 3分20秒 | 6分 |
| 第二次通话时间 | 0分 | 4分 | 3分40秒 | 4分50秒 | 0分 |
| 第三次通话时间 | 0分 | 0分 | 5分 | 2分 | 0分 |
| 应缴话费(元) | | | | | |
| 时间段 | 频数累计 | 频数 | 频率 | 累计频率 |
| 0<t≤3 | ┯ | 2 | 0.2 | 0.2 |
| 3<t≤4 | | | | |
| 4<t≤5 | | | | |
| 5<t≤6 | | | | |
| 合计 | 正 正 | | | |
| | A | B | C | D | E |
| 第一次通话时间 | 3分 | 3分45秒 | 3分55秒 | 3分20秒 | 6分 |
| 第二次通话时间 | 0分 | 4分 | 3分40秒 | 4分50秒 | 0分 |
| 第三次通话时间 | 0分 | 0分 | 5分 | 2分 | 0分 |
| 应缴话费(元) | | | | | |
| 时间段 | 频数累计 | 频数 | 频率 | 累计频率 |
| 0<t≤3 | ┯ | 2 | 0.2 | 0.2 |
| 3<t≤4 | | | | |
| 4<t≤5 | | | | |
| 5<t≤6 | | | | |
| 合计 | 正 正 | | | |
高二(3)班50名学生在一次百米测试中,成绩全部介于13秒与19秒之间,将测试结果按如下方式分成六组:第一组,成绩大于等于13秒且小于14秒;第二组,成绩大于等于14秒且小于15秒;…;第六组,成绩大于等于18秒且小于等于19秒.下图是按上述分组方法得到的频率分布直方图.设成绩小于17秒的学生人数占全班总人数的百分比为x, 成绩大于等于15秒且小于17秒的学生人数为y,则从频率分布直方图中可分析出x和y分别为( ) 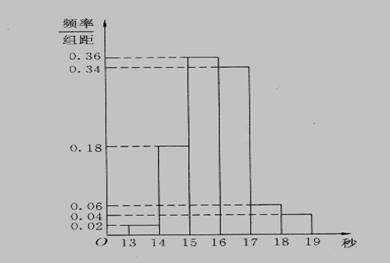
A.0.9,35 B. 0.1,45 C.0.1, 35 D. 0.9,45
高二(3)班50名学生在一次百米测试中,成绩全部介于13秒与19秒之间,将测试结果按如下方式分成六组:第一组,成绩大于等于13秒且小于14秒;第二组,成绩大于等于14秒且小于15秒;…;第六组,成绩大于等于18秒且小于等于19秒.下图是按上述分组方法得到的频率分布直方图.设成绩小于17秒的学生人数占全班总人数的百分比为x, 成绩大于等于15秒且小于17秒的学生人数为y,则从频率分布直方图中可分析出x和y分别为( ) 
| A.0.9,35 | B.0.1,45 | C.0.1, 35 | D.0.9,45 |
一.选择题:DABDA CDCBC
解析:1:由条件“函数是奇函数”可排除(B)、(C), 又 在区间
在区间 上不是单调递减, 可淘汰(A),所以选(D).
上不是单调递减, 可淘汰(A),所以选(D).
2:取满足题设的特殊数值 a= ,
, ,
,
0> ,检验不等式(B),(C),(D)均不成立,选 (A).
,检验不等式(B),(C),(D)均不成立,选 (A).
3:由已知得

4:把x=1代入不等式组验算得x=1是不等式组的解,则排除(B)、(C), 再把x=-3代入不等式组验算得x=-3是不等式组的解,则排除(B),所以选(D).
5:本题学生很容易去分母得 ,然后解方程,不易实现目标。
,然后解方程,不易实现目标。
事实上,只要利用数形结合的思想,分别画出 的图象,容易发现在第一象限没有交点。故选A。
的图象,容易发现在第一象限没有交点。故选A。
6:当m=0时,显然有 ;若
;若 时,由
时,由 ,得
,得
 ,方程无解,m不存在。故选C。
,方程无解,m不存在。故选C。
7:由已知不妨设长 宽
宽 高
高 ,则对角线的长为
,则对角线的长为 .故选
.故选
8:由 得sin(x-
得sin(x- )>0,即2 kπ<x-
)>0,即2 kπ<x- <2kπ+π,取k=0即知选C.
<2kπ+π,取k=0即知选C.
9:用特值法:当n=2时,代入得C +C
+C =2,排除答案A、C;当n=4时,代入得C
=2,排除答案A、C;当n=4时,代入得C +C
+C +C
+C =8,排除答案D。所以选B。
=8,排除答案D。所以选B。
10:考虑由P0射到BC的中点上,这样依次反射最终回到P0,此时容易求出tan =
= ,由题设条件知,1<x4<2,则tan
,由题设条件知,1<x4<2,则tan ≠
≠ ,排除A、B、D,故选C.
,排除A、B、D,故选C.
二.填空题:11、1;12、-1;13、23; 14、 ;15、
;15、 ;
;
解析:
11: 将已知方程变形为  ,
,
解这个一元二次方程,得

显然有 , 而
, 而 ,于是
,于是
原式= =
= =
=
12: 由条件得 ,其中
,其中 .
.

 是已知函数的对称轴,
是已知函数的对称轴,
 , 即
, 即  ,
,
于是  故应填
故应填  .
.
13:因为正方体是对称的几何体,所以四边形BFD1E在该正方体的面上的射影可分为:上下、左右、前后三个方向的射影,也就是在面ABCD、面ABB1A1、面ADD1A1上的射影.
四边形BFD1E在面ABCD和面ABB1A1上的射影相同,如图2所示;
四边形BFD1E在该正方体对角面的ABC1D1内,它在面ADD1A1上的射影显然是一条线段,如图3所示. 故应填23.
14.(略)
15.解:由条件不难得 为等腰直角三角形,设圆的半径为1,则
为等腰直角三角形,设圆的半径为1,则 ,
, ,
,

 ,
,
 sin∠ACO=
sin∠ACO= )=
)=
三.解答题:
16.解:(1)将 ,
, 代入函数
代入函数 得
得 ,因为
,因为 ,所以
,所以 .
------------------2分
.
------------------2分
又因为 ,
, ,
, ,所以
,所以 ,
,
因此 .
------------------5分
.
------------------5分
(2)因为点 ,
, 是
是 的中点,
的中点, , 所以点
, 所以点 的坐标为
的坐标为 . ------------------7分
. ------------------7分
又因为点 在
在 的图象上,
的图象上,
所以 .------------------9分
.------------------9分
因为 ,所以
,所以 ,
,
从而得 或
或 .即
.即 或
或 ------------------12分
------------------12分
17.解:(Ⅰ)设“甲投球一次命中”为事件A,“乙投球一次命中”为事件B
由题意得  , 解得
, 解得 或
或 (舍去),
(舍去),
所以乙投球的命中率为 ------------------3分
------------------3分
(Ⅱ)由题设和(Ⅰ)知 -------------4分
-------------4分
 可能的取值为0,1,2,3,故
可能的取值为0,1,2,3,故 


 ,
, 
 的分布列为
的分布列为

0
1
2
3





 的数学期望
的数学期望 ------------------12分
------------------12分
18.解:(1)∵
 -------------------------------------------------1分
-------------------------------------------------1分
当 时,
时,
∴函数 在
在 上为增函数-----------------------------------------3分
上为增函数-----------------------------------------3分
∴ ,
, --------------------------4分
--------------------------4分
(2)证明:令
则
∵当 时
时 ,∴函数
,∴函数 在区间
在区间 上为减函数
上为减函数
∴
即在 上,
上,
∴在区间 上,函数
上,函数 的图象在函数
的图象在函数 的图象的下方-----8分
的图象的下方-----8分
(3)证明:∵
当 时,不等式显然成立
时,不等式显然成立
当 时
时
∵ =
= -----①
-----①

 -------------②-----10分
-------------②-----10分
①+②得

≥ (当且仅当
(当且仅当 时“=”成立)---------------13分
时“=”成立)---------------13分
∴当 时,不等式成立
时,不等式成立
综上所述得 ≥
≥
 .--------------------------14分
.--------------------------14分
19.解:(Ⅰ)设 的坐标为
的坐标为 ,则
,则 且
且 .
.
解得 , 因此,点
, 因此,点  的坐标为
的坐标为 .
.
(Ⅱ) ,根据椭圆定义,
,根据椭圆定义,
得
 ,
,
 ,
, . ∴所求椭圆方程为
. ∴所求椭圆方程为 .
.
(Ⅲ) ,
, 椭圆的准线方程为
椭圆的准线方程为 .
.
设点 的坐标为
的坐标为
 ,
, 表示点
表示点 到
到 的距离,
的距离, 表示点
表示点 到椭圆的右准线的距离.
到椭圆的右准线的距离.
则 ,
, .
.
 , 令
, 令
 ,则
,则 ,
,
 当
当 ,
, ,
,  ,
, .
.
∴  在
在 时取得最小值.
时取得最小值.
因此, 最小值=
最小值= ,此时点
,此时点 的坐标为
的坐标为 -----------------14分
-----------------14分
20.解:(Ⅰ)取 中点
中点 ,连结
,连结 .
.
 为正三角形,
为正三角形, .
.
 在正三棱柱
在正三棱柱 中,平面
中,平面 平面
平面 ,
,  平面
平面 .
.
 取
取 中点
中点 ,以
,以 为原点,
为原点, ,
, ,
, 的方向为
的方向为 轴的正方向建立空间直角坐标系,则
轴的正方向建立空间直角坐标系,则 ,
, ,
, ,
, ,
,  ,
,
 ,
, ,
, .
.
 ,
, ,
,
 ,
, .
.
 平面
平面 .--------------------6分
.--------------------6分
(Ⅱ)设平面 的法向量为
的法向量为 .
.
 ,
, .
.  ,
, ,
,



令 得
得 为平面
为平面 的一个法向量.--------------------9分
的一个法向量.--------------------9分
由(Ⅰ)知 平面
平面 ,
,  为平面
为平面 的法向量.
的法向量.
 ,
, .
.
 二面角
二面角 的大小为
的大小为 . --------------------11分
. --------------------11分
(Ⅲ) 中,
中, ,
, .
.
在正三棱柱中, 到平面
到平面 的距离为
的距离为 .设点
.设点 到平面
到平面 的距离为
的距离为 .
.
由 得
得 ,
,  .
.
 点
点 到平面
到平面 的距离为
的距离为 --------------------14分
--------------------14分
21.解(1)∵不等式 ≤0的解集有且只有一个元素
≤0的解集有且只有一个元素
∴ 解得
解得 或
或 --------------------2分
--------------------2分
当 时函数
时函数 在
在 递增,不满足条件②--------------------3分
递增,不满足条件②--------------------3分
当 时函数
时函数 在(0,2)上递减,满足条件②--------------------4分
在(0,2)上递减,满足条件②--------------------4分
综上得 ,即
,即 --------------------5分
--------------------5分
(2)由(1)知 , 当
, 当 时,
时,
当 ≥2时
≥2时 =
= =
= --------------------7分
--------------------7分
∴ --------------------8分
--------------------8分
(3)由题设可得 --------------------9分
--------------------9分
∵ ,
, ,
,
∴ ,
, 都满足
都满足 --------------------11分
--------------------11分
∵当 ≥3时,
≥3时,

即当 ≥3时,数列{
≥3时,数列{ }递增,
}递增,
∵
 ,由
,由
 ,可知
,可知 满足
满足 ----------------13分
----------------13分
∴数列{ }的变号数为3. ------------------14分
}的变号数为3. ------------------14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com