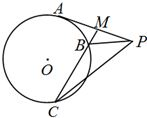选做题本题包括A，B，C，D四小题，请选定其中 两题 作答，每小题10分，共计20分，
解答时应写出文字说明，证明过程或演算步骤．
A选修4-1：几何证明选讲
自圆O外一点P引圆的一条切线PA，切点为A，M为PA的中点，过点M引圆O的割线交该圆于B、C两点，且∠BMP=100°，∠BPC=40°，求∠MPB的大小．
B选修4-2：矩阵与变换
已知二阶矩阵A=

ab cd

，矩阵A属于特征值λ₁=-1的一个特征向量为α1=

1 -1

，属于特征值λ₂=4的一个特征向量为α2=

3 2

．求矩阵A．
C选修4-4：坐标系与参数方程
在平面直角坐标系xOy中，已知曲线C的参数方程为

x=2cosα y=sinα

(α为参数)．以直角坐标系原点O为极点，x轴的正半轴为极轴建立极坐标系，直线l的极坐标方程为ρcos(θ-

π

4

)=2

2

．点
P为曲线C上的动点，求点P到直线l距离的最大值．
D选修4-5：不等式选讲
若正数a，b，c满足a+b+c=1，求

1

3a+2

+

1

3b+2

+

1

3c+2

的最小值．

查看答案和解析>>

查看答案和解析>>

查看答案和解析>>

查看答案和解析>>

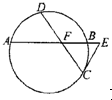选做题：（考生可以在以下三个题任选一道题作答，如果多做以考生所作的第一道题为准）
（a） 不等式|x-4|-|x-2|＞1的解集为

(-∞，

5

2

)

(-∞，

5

2

)

．
（b） 已知直线l的极坐标方程为：ρcosθ-ρsinθ-

2

=0，圆C的参数方程为

x=cosθ y=sinθ

（θ为参数），那么直线l与圆C的位置关系为

相切

相切

．
（c） 如图已知圆中两条弦AB与CD相交于点F，E是AB延长线上一点，且DF=CF=

2

，AF：FB：BE=4：2：1．若CE与圆相切，则CE的长为

7

2

7

2

．

查看答案和解析>>

一．选择题：DABDA CDCBC

解析：1:由条件“函数是奇函数”可排除(B)、(C), 又在区间上不是单调递减, 可淘汰(A)，所以选(D).

2：取满足题设的特殊数值 a=,，

0>,检验不等式(B),(C),(D)均不成立,选 (A).

3：由已知得

4：把x=1代入不等式组验算得x=1是不等式组的解，则排除(B)、(C), 再把x=-3代入不等式组验算得x=-3是不等式组的解，则排除(B)，所以选(D).

5：本题学生很容易去分母得，然后解方程，不易实现目标。

事实上，只要利用数形结合的思想，分别画出的图象，容易发现在第一象限没有交点。故选A。

6：当m=0时，显然有；若时，由，得，方程无解，m不存在。故选C。

7：由已知不妨设长宽高，则对角线的长为.故选

8：由得sin（x－）＞0，即2 kπ＜x－＜2kπ＋π，取k＝0即知选C.

9：用特值法：当n＝2时，代入得C＋C＝2,排除答案A、C；当n＝4时，代入得C＋C＋C＝8,排除答案D。所以选B。

10：考虑由P₀射到BC的中点上，这样依次反射最终回到P₀，此时容易求出tan=，由题设条件知，1＜x₄＜2，则tan≠，排除A、B、D，故选C.

二．填空题：11、1；12、-1；13、23； 14、；15、；

解析：

11：　将已知方程变形为　　，

解这个一元二次方程，得

    显然有,　而,于是

    原式＝ ＝＝

12：　由条件得，其中.

是已知函数的对称轴，

，   即　　，

于是　　故应填 .

13：因为正方体是对称的几何体，所以四边形BFD₁E在该正方体的面上的射影可分为：上下、左右、前后三个方向的射影，也就是在面ABCD、面ABB₁A₁、面ADD₁A₁上的射影.

四边形BFD₁E在面ABCD和面ABB₁A₁上的射影相同，如图2所示；

四边形BFD₁E在该正方体对角面的ABC₁D₁内，它在面ADD₁A₁上的射影显然是一条线段，如图3所示.  故应填23.

14.（略）

15.解：由条件不难得为等腰直角三角形，设圆的半径为1，则，，

，   sin∠ACO=）=

三．解答题：

16.解：（1）将，代入函数得，因为，所以．                             ------------------2分

又因为，，，所以，

 因此．               ------------------5分

（2）因为点，是的中点，， 所以点的坐标为．      ------------------7分

又因为点在的图象上，

所以．------------------9分

因为，所以，

从而得或．即或 ------------------12分

17.解：（Ⅰ）设“甲投球一次命中”为事件A，“乙投球一次命中”为事件B

由题意得  ， 解得或（舍去），

所以乙投球的命中率为                  ------------------3分

（Ⅱ）由题设和（Ⅰ）知-------------4分

可能的取值为0，1，2，3，故

 ， 

的分布列为

0

1

2

3

的数学期望  ------------------12分

18.解：(1)∵-------------------------------------------------1分

当时，

∴函数在上为增函数-----------------------------------------3分

∴，--------------------------4分

（２）证明：令

则

∵当时，∴函数在区间上为减函数

∴

即在上，

∴在区间上，函数的图象在函数的图象的下方-----8分

（3）证明：∵

当时，不等式显然成立

当时

∵＝-----①

-------------②-----10分

①+②得

≥（当且仅当时“＝”成立）---------------13分

∴当时，不等式成立

综上所述得≥ .--------------------------14分

19.解：（Ⅰ）设的坐标为，则且．

解得，  因此，点 的坐标为．

（Ⅱ），根据椭圆定义，

得，

，．    ∴所求椭圆方程为．

（Ⅲ），椭圆的准线方程为．

设点的坐标为,表示点到的距离，表示点到椭圆的右准线的距离．

则，．

， 令，则，

当，， ，．

 ∴ 在时取得最小值．

因此，最小值＝，此时点的坐标为-----------------14分

20.解：（Ⅰ）取中点，连结．

为正三角形，．

在正三棱柱中，平面平面， 平面．

取中点，以为原点，，，的方向为轴的正方向建立空间直角坐标系，则，，，，    ，

，，．

，，

，．

平面．--------------------6分

（Ⅱ）设平面的法向量为．

，．  ，，

令得为平面的一个法向量．--------------------9分

由（Ⅰ）知平面， 为平面的法向量．

，．

二面角的大小为．   --------------------11分

（Ⅲ）中，，．

在正三棱柱中，到平面的距离为．设点到平面的距离为．

由得， ．

点到平面的距离为--------------------14分

21.解（１）∵不等式≤0的解集有且只有一个元素

∴　解得或 --------------------2分

当时函数在递增，不满足条件②--------------------3分

当时函数在（０，２）上递减，满足条件②--------------------4分

综上得，即   --------------------5分

（２）由（１）知,    当时，

当≥２时＝＝  --------------------7分

∴    --------------------8分

（３）由题设可得--------------------9分

∵，，

∴，都满足     --------------------11分

∵当≥３时，

即当≥３时，数列｛｝递增，

∵，由，可知满足----------------13分

∴数列｛｝的变号数为３.         ------------------14分