
18.解:(Ⅰ)证明:∵PA⊥平面ABCD ∴PA⊥BD
∵ABCD为正方形 ∴AC⊥BD
∴BD⊥平面PAC又BD在平面BPD内,
∴平面PAC⊥平面BPD 6分
(Ⅱ)解法一:在平面BCP内作BN⊥PC垂足为N,连DN,
∵Rt△PBC≌Rt△PDC,由BN⊥PC得DN⊥PC;
∴∠BND为二面角B―PC―D的平面角,
在△BND中,BN=DN= ,BD=
,BD=
∴cos∠BND = 12分
12分
解法二:以A为原点,AB、AD、AP所在直线分别为x轴、y轴、z轴建立空间坐标系如图,在平面BCP内作BN⊥PC垂足为N连DN,
∵Rt△PBC≌Rt△PDC,由BN⊥PC得DN⊥PC;
∴∠BND为二面角B―PC―D的平面角 8分
设

 10分
10分
 12分
12分
解法三:以A为原点,AB、AD、AP所在直线分别为x轴、y轴、z轴建立如图空间坐标系,作AM⊥PB于M、AN⊥PD于N,易证AM⊥平面PBC,AN⊥平面PDC,


 10分 10分
∵二面角B―PC―D的平面角与∠MAN互补 ∴二面角B―PC―D的余弦值为 12分 12分 19.解:(Ⅰ) 
 4分 4分
又∵当n = 1时,上式也成立, 6分 6分 (Ⅱ) 8分 8分 又 
 ①
①
 ②
②
①-②得: 
 12分 12分
20.解:(Ⅰ)由 知M是AB的中点, 知M是AB的中点, 设A、B两点的坐标分别为 由  , ,
∴M点的坐标为 4分 4分 又M点的直线l上: 
 7分 7分
(Ⅱ)由(Ⅰ)知 ,不妨设椭圆的一个焦点坐标为 ,不妨设椭圆的一个焦点坐标为 关于直线l: 关于直线l:  上的对称点为 上的对称点为 , ,
则有 10分 10分 由已知  ,∴所求的椭圆的方程为 ,∴所求的椭圆的方程为 12分 12分
21.解:(Ⅰ)∵函数f(x)图象关于原点对称,∴对任意实数x有 , ,  , ,
即 2分 2分 
 4分 4分
(Ⅱ)当 时,图象上不存在这样的两点使结论成立 5分 时,图象上不存在这样的两点使结论成立 5分 假设图象上存在两点 ,使得过此两点处的切线互相垂直,则由 ,使得过此两点处的切线互相垂直,则由  ,知两点处的切线斜率分别为: ,知两点处的切线斜率分别为:


此与(*)相矛盾,故假设不成立 9分 (Ⅲ)证明: , , 
 在[-1,1]上是减函数,且 在[-1,1]上是减函数,且
∴在[-1,1]上, 时, 时,  14分 14分
| |

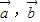 满足
满足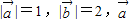 与
与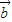 的夹角为60°,则
的夹角为60°,则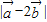 = .
= .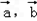 满足
满足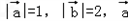 与
与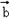 的夹角为60°,则
的夹角为60°,则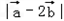 =( ).
=( ).![]() 满足
满足![]() 与
与![]() 的夹角为60°,则
的夹角为60°,则![]()
![]() ___
___![]() ___________.
___________.![]() ,
,![]() 满足
满足![]()
![]() 与
与![]() 的夹角为60°,则“m=1”是“
的夹角为60°,则“m=1”是“![]() ”的
”的![]() ,
,![]() 满足
满足![]()
![]() 与
与![]() 的夹角为60°,则“m=1”是“
的夹角为60°,则“m=1”是“![]() ”的
”的