
题目列表(包括答案和解析)
已知在等差数列{an}中,a1=120,d=-4,若Sn≤an(n≥2),则n的最小值为
A.60
B.62
C.70
D.72
| A、60 | B、62 | C、70 | D、72 |
已知 是等差数列,d为公差且不为0,a1和d均为实数,它的前n项和记作Sn,设集合
是等差数列,d为公差且不为0,a1和d均为实数,它的前n项和记作Sn,设集合 .试问下列命题是否是真命题,如果是真命题,请给予证明;如果是假命题,请举反例说明.
.试问下列命题是否是真命题,如果是真命题,请给予证明;如果是假命题,请举反例说明.
(1)若以集合A中的元素作为点的坐标,则这些点都在同一条直线上;
(2) 至多有一个元素;
至多有一个元素;
(3)当a1≠0时,一定有 .
.
已知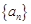 是等差数列,d为公差且不为0,a1和d均为实数,它的前n项和记作Sn,设集合
是等差数列,d为公差且不为0,a1和d均为实数,它的前n项和记作Sn,设集合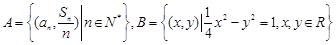 .试问下列命题是否是真命题,如果是真命题,请给予证明;如果是假命题,请举反例说明.
.试问下列命题是否是真命题,如果是真命题,请给予证明;如果是假命题,请举反例说明.
(1)若以集合A中的元素作为点的坐标,则这些点都在同一条直线上;
(2)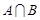 至多有一个元素;
至多有一个元素;
(3)当a1≠0时,一定有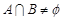 .
.
| A.60 | B.62 | C.70 | D.72 |
一、选择题:
1.D 2.C 3.A 4.A 5.B 6.A 7.B 8.C 9.B 10.C
11.B 12.C
二、选择题;
|