
题目列表(包括答案和解析)
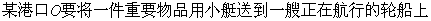 。
。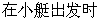 ,轮船位于港口O北偏西
,轮船位于港口O北偏西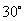 且与该港口相距20海里的A处,并以30海里/小时的航行速度沿正东方向匀速行驶。假设该小船沿直线方向以
且与该港口相距20海里的A处,并以30海里/小时的航行速度沿正东方向匀速行驶。假设该小船沿直线方向以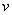 海里/小时的航行速度匀速行驶,经过t小时与轮船相遇。
海里/小时的航行速度匀速行驶,经过t小时与轮船相遇。
(1)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?
(2)假设小艇的最高航行速度只能达到30海里/小时,试设计航行方案(即确定航行方向与航行速度的大小),使得小艇能以最短时间与轮船相遇,并说明理由。
已知函数 。
。
(1)求函数的最小正周期和最大值;
(2)求函数的增区间;
(3)函数的图象可以由函数 的图象经过怎样的变换得到?
的图象经过怎样的变换得到?
【解析】本试题考查了三角函数的图像与性质的运用。第一问中,利用 可知函数的周期为
可知函数的周期为 ,最大值为
,最大值为 。
。
第二问中,函数 的单调区间与函数
的单调区间与函数 的单调区间相同。故当
的单调区间相同。故当 ,解得x的范围即为所求的区间。
,解得x的范围即为所求的区间。
第三问中,利用图像将 的图象先向右平移
的图象先向右平移 个单位长度,再把横坐标缩短为原来的
个单位长度,再把横坐标缩短为原来的 (纵坐标不变),然后把纵坐标伸长为原来的
(纵坐标不变),然后把纵坐标伸长为原来的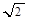 倍(横坐标不变),再向上平移1个单位即可。
倍(横坐标不变),再向上平移1个单位即可。
解:(1)函数 的最小正周期为
的最小正周期为 ,最大值为
,最大值为 。
。
(2)函数 的单调区间与函数
的单调区间与函数 的单调区间相同。
的单调区间相同。
 即
即
 所求的增区间为
所求的增区间为 ,
,
 即
即
 所求的减区间为
所求的减区间为 ,
, 。
。
(3)将 的图象先向右平移
的图象先向右平移 个单位长度,再把横坐标缩短为原来的
个单位长度,再把横坐标缩短为原来的 (纵坐标不变),然后把纵坐标伸长为原来的
(纵坐标不变),然后把纵坐标伸长为原来的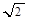 倍(横坐标不变),再向上平移1个单位即可。
倍(横坐标不变),再向上平移1个单位即可。
已知函数 在
在 取得极值
取得极值
(1)求 的单调区间(用
的单调区间(用 表示);
表示);
(2)设 ,
, ,若存在
,若存在 ,使得
,使得 成立,求
成立,求 的取值范围.
的取值范围.
【解析】第一问利用

根据题意 在
在 取得极值,
取得极值, 
对参数a分情况讨论,可知
当 即
即 时递增区间:
时递增区间:  递减区间:
递减区间:  ,
,

当 即
即 时递增区间:
时递增区间:  递减区间:
递减区间:  ,
,

第二问中, 由(1)知:
由(1)知:  在
在 ,
,

 ,
,
 在
在


从而求解。
解: 
 …..3分
…..3分
 在
在 取得极值,
取得极值,  ……………………..4分
……………………..4分
(1) 当 即
即 时 递增区间:
时 递增区间:  递减区间:
递减区间:  ,
,

当 即
即 时递增区间:
时递增区间:  递减区间:
递减区间:  ,
,
 ………….6分
………….6分
(2)  由(1)知:
由(1)知:  在
在 ,
,

 ,
,
 在
在

 ……………….10分
……………….10分
 , 使
, 使 成立
成立



 得:
得: 
设 ,
, 且为常数。若存在一公差大于
且为常数。若存在一公差大于 的等差数列
的等差数列 ,使得
,使得 为一公比大于
为一公比大于 的等比数列,请写出满足条件的一组
的等比数列,请写出满足条件的一组 的值 .(答案不唯一,一组即可)
的值 .(答案不唯一,一组即可)
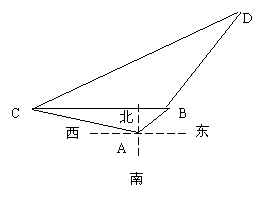 在海岸A处测得北偏东
在海岸A处测得北偏东![]() 方向,距A为
方向,距A为![]() km的B处有一鱼群,鱼群正以10 km / h的速度从B处向北偏东
km的B处有一鱼群,鱼群正以10 km / h的速度从B处向北偏东![]() 方向游动.在A处北偏西
方向游动.在A处北偏西![]() 方向,离A为2 km的C处有一艘渔船获悉立即以
方向,离A为2 km的C处有一艘渔船获悉立即以![]() km/ h的速度追捕鱼群,问渔船沿什么方向行驶才能最快追上鱼群?并求出所需时间。
km/ h的速度追捕鱼群,问渔船沿什么方向行驶才能最快追上鱼群?并求出所需时间。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com