
题目列表(包括答案和解析)
| 1 |
| 500 |
| ? |
| y |
| ? |
| b |
| ? |
| a |
| . |
| x |
| . |
| y |
| A.①②③ | B.②③ | C.②③④ | D.①②③④ |
三、解答题:解答应写出文字说明、证明过程或演算步骤(本大题共6个大题,共76分)。
17.(12分)以下资料是一位销售经理收集来的每年销售额和销售经验年数的关系:
|
销售经验(年) |
1 |
3 |
4 |
4 |
6 |
8 |
10 |
10 |
11 |
13 |
|
年销售额(千元) |
80 |
97 |
92 |
102 |
103 |
111 |
119 |
123 |
117 |
136 |
(1)依据这些数据画出散点图并作直线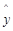 =78+4.2x,计算
=78+4.2x,计算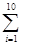 (yi-
(yi-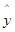 i)2;
i)2;
(2)依据这些数据由最小二乘法求线性回归方程,并据此计算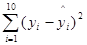 ;
;
(3)比较(1)和(2)中的残差平方和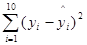 的大小.
的大小.
三、解答题:解答应写出文字说明、证明过程或演算步骤(本大题共6个大题,共76分)。
17.(12分)以下资料是一位销售经理收集来的每年销售额和销售经验年数的关系:
| 销售经验(年) | 1 | 3 | 4 | 4 | 6 | 8 | 10 | 10 | 11 | 13 |
| 年销售额(千元) | 80 | 97 | 92 | 102 | 103 | 111 | 119 | 123 | 117 | 136 |
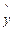 =78+4.2x,计算
=78+4.2x,计算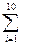 (yi-
(yi-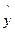 i)2;
i)2; 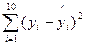 ;
;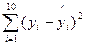 的大小.
的大小.一、填空题:
1. ; 2.
; 2. ; 3.
; 3. ; 4.
; 4. ; 5.
; 5. ;
;
6. ; 7.
; 7. 8.
8. ; 9.21; 10.
; 9.21; 10. ;
;
11. ;12.
;12. ; 13.
; 13. ; 14.
; 14.
二、解答题:
15.(1)编号为016; ----------------------------3分
(2)
分组
频数
频率
60.5~70.5
8
0.16
70.5~80.5
10
0.20
80.5~90.5
18
0.36
90.5~100.5
14
0.28
合计
50
1

------------- ----------------------------8分
(3)在被抽到的学生中获二奖的人数是9+7=16人,
占样本的比例是 ,即获二等奖的概率约为32%,
,即获二等奖的概率约为32%,
所以获二等奖的人数估计为800×32%=256人。有 ------------------------13分
答:获二等奖的大约有256人。 -----------------------------------14分
16.解:(1) B=600,A+C=1200, C=1200 -A,
∴ sinA-sinC+ cos(A-C)
cos(A-C)
= sinA-
sinA- cosA+
cosA+ [1-2sin2(A-60°)]=
[1-2sin2(A-60°)]= ,
,
∴sin(A-60°)[1- sin(A-60°)]=0?
-------------------------4分
sin(A-60°)]=0?
-------------------------4分
∴sin(A-60°)=0或sin(A-60°)= , 又0°<A<120°,
, 又0°<A<120°,
∴A=60°或105°.??? -------------------------8分
(2) 当A=60°时,S△= acsinB=
acsinB= ×4R2sin360°=
×4R2sin360°= ------------11分
------------11分
当A=105°时,?S△= ×4R2?sin105°sin15°sin60°=
×4R2?sin105°sin15°sin60°= ----------------14分
----------------14分
17.解:(1)如四面体A1-ABC或四面体C1-ABC或四面体A1-ACD或四面体C1-ACD; ---4分
(2)如四面体B1-ABC或四面体D1-ACD; -------------------------8分
(3)如四面体A-B1CD1(3分 ); -------------------------11分
设长方体的长、宽、高分别为 ,则
,则 .---------14分
.---------14分
18.(1)如图,由光学几何知识可知,点 关于
关于 的对称点
的对称点 在过点
在过点 且倾斜角为
且倾斜角为 的直线
的直线 上。在
上。在 中,椭圆长轴长
中,椭圆长轴长 , ----4分
, ----4分
又椭圆的半焦距 ,∴
,∴ ,
,
∴所求椭圆的方程为 .
-----------------------------7分
.
-----------------------------7分
(2)路程最短即为 上上的点
上上的点 到圆
到圆 的切线长最短,由几何知识可知,
的切线长最短,由几何知识可知, 应为过原点
应为过原点 且与
且与 垂直的直线与
垂直的直线与 的交点,这一点又与点
的交点,这一点又与点 关于
关于 对称,∴
对称,∴ ,故点
,故点 的坐标为
的坐标为 .
-------------------------15分
.
-------------------------15分
注:用代数方法求解同样分步给分!

19. 解:(1)若 ,对于正数
,对于正数 ,
, 的定义域为
的定义域为 ,但
,但 的值域
的值域 ,故
,故 ,不合要求. --------------------------2分
,不合要求. --------------------------2分
若 ,对于正数
,对于正数 ,
, 的定义域为
的定义域为 . -----------------3分
. -----------------3分
由于此时 ,
,
故函数的值域 .
------------------------------------6分
.
------------------------------------6分
由题意,有 ,由于
,由于 ,所以
,所以 .------------------8分
.------------------8分

20.解:(1)依题意数列 的通项公式是
的通项公式是 ,
,
故等式即为 ,
,
同时有
 ,
,
两式相减可得 ------------------------------3分
------------------------------3分
可得数列 的通项公式是
的通项公式是 ,
,
知数列 是首项为1,公比为2的等比数列。 ---------------------------4分
是首项为1,公比为2的等比数列。 ---------------------------4分
(2)设等比数列 的首项为
的首项为 ,公比为
,公比为 ,则
,则 ,从而有:
,从而有:
 ,
,
又
 ,
,
故 -----------------------------6分
-----------------------------6分
 ,
,
要使 是与
是与 无关的常数,必需
无关的常数,必需 , ----------------------------8分
, ----------------------------8分
即①当等比数列 的公比
的公比 时,数列
时,数列 是等差数列,其通项公式是
是等差数列,其通项公式是 ;
;
②当等比数列 的公比不是2时,数列
的公比不是2时,数列 不是等差数列. ------------9分
不是等差数列. ------------9分
(3)由(2)知 , ------------------------------------------10分
, ------------------------------------------10分


 --------------14分
--------------14分



 ----------------------------16分
----------------------------16分
|