解析：本例主要是培养学生理解概念的程度，了解解决数学问题都需要算法

算法一：按照逐一相加的程序进行.

第一步　计算1＋2，得到3；

第二步　将第一步中的运算结果3与3相加，得到6；

第三步　将第二步中的运算结果6与4相加，得到10；

第四步　将第三步中的运算结果10与5相加，得到15；

第五步　将第四步中的运算结果15与6相加，得到21；

第六步　将第五步中的运算结果21与7相加，得到28.

算法二：可以运用公式1＋2＋3＋…＋n＝直接计算.

第一步　取n＝7；

第二步　计算；

第三步　输出运算结果.

解析：对任意x₁，x₂∈[0，＋∞)(x₁≠x₂)，有<0，实际上等价于函数f(x)在[0，＋∞)上是减函数，故f(3)<f(2)<f(1)，由于函数是偶函数，故f(3)<f(－2)<f(1)．

答案：A

解析：依题意得f(x)的图象关于直线x＝1对称，f(x＋1)＝－f(x－1)，f(x＋2)＝－f(x)，f(x＋4)＝－f(x＋2)＝f(x)，即函数f(x)是以4为周期的函数．由f(x)在[3,5]上是增函数与f(x)的图象关于直线x＝1对称得，f(x)在[－3，－1]上是减函数．又函数f(x)是以4为周期的函数，因此f(x)在[1,3]上是减函数，f(x)在[1,3]上的最大值是f(1)，最小值是f(3)．

答案：A

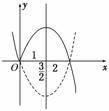解析：y＝－(x－3)|x|

＝

作出该函数的图象，观察图象知递增区间为[0，]．

答案：[0，]

4．D解析：函数f(x)=0在区间(a,b)上恰有一解，函数在(a,b)上的图象也可能不单调如图

有以下一组数据：

有以下四种函数，其中拟合最好的函数是（　　）

A.    B.    C.  D.