下列根式、分数指数幂的互化中，正确的是(　　)

A.-=(x≠0)

B.=-

C.()=(xy≠0)

D.= (y<0)

A. -（x≠0）                          B.

C.（xy≠0）                    D.（y＜0

在平面直角坐标系xoy中，已知曲线C₁：x²+y²=1，以平面直角坐标系xoy的原点O为极点，x轴的正半轴为极轴，取相同的单位长度建立极坐标系，已知直线l：ρ(2cosθ-sinθ)=6.

（Ⅰ）将曲线C₁上的所有点的横坐标，纵坐标分别伸长为原来的、2倍后得到曲线C₂，试写出直线l的直角坐标方程和曲线C₂的参数方程.

（Ⅱ）在曲线C₂上求一点P，使点P到直线l的距离最大，并求出此最大值．

【解析】（Ⅰ）根据极坐标与普通方程的互化，将直线l：ρ(2cosθ-sinθ)=6化为普通方程，C₂的方程为，化为普通方程；（Ⅱ）利用点到直线的距离公式表示出距离，求最值.

已知函数

（1）若函数的图象经过P（3，4）点，求a的值；

（2）比较大小，并写出比较过程；

（3）若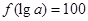，求a的值.

【解析】本试题主要考查了指数函数的性质的运用。第一问中，因为函数的图象经过P（3，4）点，所以，解得，因为，所以.

（2）问中，对底数a进行分类讨论，利用单调性求解得到。

（3）中，由知，.，指对数互化得到，，所以，解得所以， 或 .

解：⑴∵函数的图象经过∴，即.        … 2分

又，所以.             ………… 4分

⑵当时，;

当时，. ……………… 6分

因为，，

当时，在上为增函数，∵，∴.

即.当时，在上为减函数，

∵，∴.即.      …………………… 8分

⑶由知，.所以，（或）.

∴.∴，       … 10分

∴ 或 ，所以， 或 .