
题目列表(包括答案和解析)
由曲线 和
和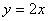 围成图形的面积为 。
围成图形的面积为 。
由曲线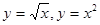 所围成图形的面积是________ 。
所围成图形的面积是________ 。
|
|
(本大题共分12分)
已知曲线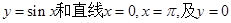 所围成图形的面积为
所围成图形的面积为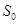 .
.
(1)求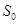 .
.
(2)求所围成图形绕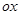 轴旋转所成旋转体的体积。
轴旋转所成旋转体的体积。
(本大题共分1 2分)
2分)
已知曲线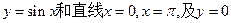 所围成图形的面积为
所围成图形的面积为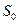 .
.
(1)求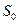 .
.
(2)求所围成图形绕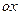 轴旋转所成旋转体的体积。
轴旋转所成旋转体的体积。
一、 选择题:1. A 2. B 3. D 4. B 5. A 6. A 7. C 8. C 9. D 10. C
11. C 12. B
二、 填空题:13. 7;14. 111;15. 323;16. 3
三、 解答题:
17. 解:(1) ∵f(0)=8,
∴ ………………2分
………………2分
即 ∴
∴ ………………………6分
………………………6分
(2) 由(1)知: …………………7分
…………………7分
 ……………………8分
……………………8分
 …………………9分
…………………9分
 ………………………10分
………………………10分
∴ ,此时
,此时 (k∈Z)………………………11分
(k∈Z)………………………11分
即 (k∈Z)时,
(k∈Z)时, .……………………………12分
.……………………………12分
18. 解:(1) 
 ,
, …3分
…3分
∴分布列为:

0
1
2




………………………………………………5分
∴ ……………………………7分
……………………………7分
(2)  ……………………12分
……………………12分
19. 解:(1) 设数列 的前n项和为
的前n项和为 ,由题意知:
,由题意知:
即? ,两式相减可得:
,两式相减可得: ………………………2分
………………………2分
∴ (n∈
(n∈ )…………………………4分
)…………………………4分
设数列 的前n项和为
的前n项和为 ,由题意知:
,由题意知: ,即
,即
两式相除可得: ,则
,则 ………………………6分
………………………6分
∴ (n∈
(n∈ )………………………8分
)………………………8分
(2) 假设存在,则 ,
,

 为正整数.
为正整数.
故存在p,满足 ………………12分
………………12分
20. 解法一:(1) 连结 交BD于F.
交BD于F.
 ∵D为
∵D为 中点,
中点, ,
,
∴ ,
,
Rt△BCD∽Rt△ ,∴∠
,∴∠ =∠CDB,
=∠CDB,
∴ ⊥BD………………2分
⊥BD………………2分
∵直三棱柱 中,平面ABC⊥平面
中,平面ABC⊥平面 ,
,
又AC⊥BC,∴AC⊥平面 ,∴AC⊥BD,
,∴AC⊥BD,
AC∩ =C,BD⊥平面
=C,BD⊥平面 ,∴
,∴ ⊥BD…………………4分
⊥BD…………………4分
又在正方形 中,
中, ⊥
⊥ …………………………………5分
…………………………………5分
∴ ⊥平面
⊥平面 .……………………………6分
.……………………………6分
(2) 设 与
与 交于点M,AC=1,连结AF、MF,
交于点M,AC=1,连结AF、MF,
由(1)知BD⊥平面 ,∴MF⊥BD,AF⊥BD,
,∴MF⊥BD,AF⊥BD,
∴∠AFM是二面角A-BD- 的平面角………………………9分
的平面角………………………9分
在Rt△AFB中,AB= ,BF=
,BF= ,∠AFB
= 90°,
,∠AFB
= 90°,
∴AF= ,又
,又 ,∠AMF
= 90°,∴sin∠AFM=
,∠AMF
= 90°,∴sin∠AFM= ,∴∠AFM=
,∴∠AFM= ,
,
故二面角A-BD- 的大小为
的大小为 .…………………………12分
.…………………………12分
方法二:直三棱柱 中,∠ACB=90°,
中,∠ACB=90°,
以C为原点O,CB、 、CA分别为x轴、y轴、z轴建立空间直角坐标系如图,设AC=2,
、CA分别为x轴、y轴、z轴建立空间直角坐标系如图,设AC=2,
则B(2,0,0), ,
, ,A(0,0,2),D(0,
,A(0,0,2),D(0,  ,0)…………………2分
,0)…………………2分
(1)  ,
, ,
, ,
,
 ,
, ,…………………4分
,…………………4分
∴ ⊥BD,
⊥BD, ⊥
⊥ ,又
,又 ∩BD=D,
∩BD=D,
∴ ⊥平面
⊥平面 ;……………………………6分
;……………………………6分
 (2) 由(1)知
(2) 由(1)知 ⊥平面
⊥平面 ,且
,且 ,…8分
,…8分
设 ,且
,且 ⊥
⊥ ,
, ⊥
⊥
∵ ,
, ,
,
∴ ,
, ,即2x-2z=0,-2x+2y=0,令x=1,
,即2x-2z=0,-2x+2y=0,令x=1,
得平面ABD的一法向量 ,………………10分
,………………10分
又 ,∴
,∴ ,
,
∴二面角 的大小为
的大小为 .…………………………………12分
.…………………………………12分
21. 解:(1) 设P(x,y)代入 得点P的轨迹方程为
得点P的轨迹方程为 .……5分
.……5分
(2) 设过点C的直线斜率存在时的方程为 ,且A(
,且A( ),B(
),B( )在
)在 上,则由
上,则由 代入
代入 得
得
 .…………………6分
.…………………6分
∴ ,
, .
.
∴ .………………8分
.………………8分
令 ,∴
,∴ =
=
 .…8分
.…8分
∵ ≥0,∴
≥0,∴ ≤
≤ <0,∴
<0,∴ .………………10分
.………………10分
当过点C的直线斜率不存在时,其方程为x=-1,解得 ,
, .此时
.此时 .11分
.11分
所以 的取值范围为
的取值范围为 .………………12分
.………………12分
22. 解:(1)  ……3分
……3分
∵ >0.以下讨论函数
>0.以下讨论函数 的情况.
的情况.
① 当a≥0时, ≤-1<0,即
≤-1<0,即 <0.
<0.
所以 在R上是单调递减的.…………………………5分
在R上是单调递减的.…………………………5分
② 当a<0时, 的两根分别为
的两根分别为 且
且 <
< .
.
在(-∞,  )和(
)和( ,+∞)上
,+∞)上 >0,即
>0,即 >0.
>0.
所以函数 的递增区间为(-∞,
的递增区间为(-∞,  )和(
)和( ,+∞);
,+∞);
同理函数f(x)的递减区间为( ,
, ).………………9分
).………………9分
综上所述:当a≥0时, 在R上是单调递减的;
在R上是单调递减的;
当a<0时, 在(-∞,
在(-∞,  )和(
)和( ,+∞)上单调递增,
,+∞)上单调递增,
在( ,
, )上是单调递减的.………………………10分
)上是单调递减的.………………………10分
(2) 当-1<a<0时,
 <1,
<1,  =
= >2,………12分
>2,………12分
∴当x∈[1,2]时, 是单调递减的.………………13分
是单调递减的.………………13分
∴ . ………………………………14分
. ………………………………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com