
题目列表(包括答案和解析)
 [选做题]在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.
[选做题]在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.
|
|
| π |
| 4 |
| 2 |
| c |
| 4 |
| c |
| 6 |
 对应的变换作用下得到的曲线C′的方程.
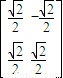
对应的变换作用下得到的曲线C′的方程.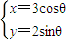 (θ为参数)和曲线C2:ρsin(θ-
(θ为参数)和曲线C2:ρsin(θ-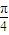 )=
)=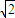 .
.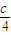 ,|y-b|<
,|y-b|<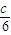 ,求证:|2x-3y-2a+3b|<c.
,求证:|2x-3y-2a+3b|<c.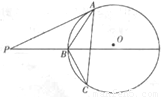
| x2 |
| a2 |
| y2 |
| b2 |
| OA |
| OB |
| 0 |
| AF2 |
| F1F2 |
| ||
| 2 |
A、y=
| ||||
B、y=-
| ||||
C、y=-
| ||||
D、y=
|
| x2 |
| a2 |
| y2 |
| b2 |
| OA |
| OB |
| 0 |
| AF2 |
| F1F2 |
| ||
| 2 |
A.y=
| B.y=-
| C.y=-
| D.y=
|
已知F1、F2分别是椭圆![]() +
+![]() =1(a>b>0)的左、右焦点,A是椭圆上位于第一象限内的一点,点B也在椭圆上,且满足
=1(a>b>0)的左、右焦点,A是椭圆上位于第一象限内的一点,点B也在椭圆上,且满足![]() +
+![]() =0(O为坐标原点),
=0(O为坐标原点),![]() ·
·![]() =0,若椭圆的离心率等于
=0,若椭圆的离心率等于![]() ,则直线AB的方程是( )
,则直线AB的方程是( )
(A)y=![]() x (B)y=-
x (B)y=-![]() x
x
![]() (C)y=-
(C)y=-![]() x (D)y=
x (D)y=![]() x
x
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com