
题目列表(包括答案和解析)
(08年聊城市四模理) (14分) 在直角坐标平面上有一点列![]() 位于直线
位于直线![]() 上,且Pn的横坐标构成以
上,且Pn的横坐标构成以![]() 为首项,-1为公差的等差数列{xn}.
为首项,-1为公差的等差数列{xn}.
(1)求点Pn的坐标;
(2)设抛物线列C1,C2,…,Cn,…中的每一条的对称轴都垂直于x轴,第n条抛物线Cn的顶点为Pn,且经过点Dn(0,n2+1)![]() . 记与抛物线Cn相切于点Dn的直线的斜率为kn,求证:
. 记与抛物线Cn相切于点Dn的直线的斜率为kn,求证:![]() ;
;
(3)设![]() ,等差数列{an}的任意一项
,等差数列{an}的任意一项![]() ,其中a1是S∩T中的最大数,且-256<a10<-125,求数列{an}通项公式.
,其中a1是S∩T中的最大数,且-256<a10<-125,求数列{an}通项公式.
(本小题满分12分)在直角坐标平面上有一点列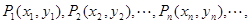 对一切正整数n,点Pn在函数
对一切正整数n,点Pn在函数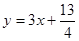 的图象上,且Pn的横坐标构成以
的图象上,且Pn的横坐标构成以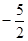 为首项,-1为公差的等差数列{xn}.
为首项,-1为公差的等差数列{xn}.
(1)求点Pn的坐标;
(2)设抛物线列C1,C2,C3,…,Cn,…中的每一条的对称轴都垂直于x轴,抛物线Cn的顶点为Pn,且过点Dn(0, ).记与抛物线Cn相切于点Dn的直线的斜率为kn,求
).记与抛物线Cn相切于点Dn的直线的斜率为kn,求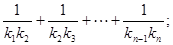
(3)设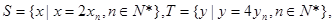 等差数列
等差数列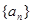 的任一项
的任一项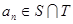 ,其中
,其中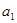 是
是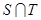 中的最大数,
中的最大数,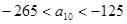 ,求数列
,求数列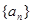 的通项公式.
的通项公式.
(本小题满分12分)在直角坐标平面上有一点列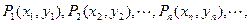 对一切正整数n,点Pn在函数
对一切正整数n,点Pn在函数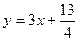 的图象上,且Pn的横坐标构成以
的图象上,且Pn的横坐标构成以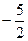 为首项,-1为公差的等
为首项,-1为公差的等 差数列{xn}.
差数列{xn}.
(1)求点Pn的坐标;
(2)设抛物线列C1,C2,C3,…,Cn,…中的每一条的对称轴都垂直于x轴,抛物线Cn的顶点为Pn,且过点Dn(0,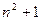 ).记与抛物线Cn相切于点Dn的直线的斜率为kn,求
).记与抛物线Cn相切于点Dn的直线的斜率为kn,求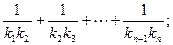
(3) 设
设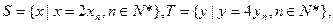 等差数列
等差数列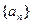 的任一项
的任一项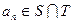 ,其中
,其中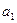 是
是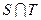 中的最大数,
中的最大数,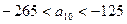 ,求数列
,求数列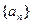 的通项公式.
的通项公式.
在直角坐标平面上有一点列
![]() 对一切正整数n,点Pn在函数
对一切正整数n,点Pn在函数![]() 的图象上,且Pn的横坐标构成以
的图象上,且Pn的横坐标构成以![]() 为首项,-1为公差的等差数列{xn}.
为首项,-1为公差的等差数列{xn}.
(1)求点Pn的坐标;
(2)设抛物线列C1,C2,C3,…,Cn,…中的每一条的对称轴都垂直于x轴,抛物线Cn的顶点为Pn,且过点Dn(0,![]() ).记与抛物线Cn相切于点Dn的直线的斜率为kn,求
).记与抛物线Cn相切于点Dn的直线的斜率为kn,求![]()
(3)设![]() 等差数列
等差数列![]() 的任一项
的任一项![]() ,其中
,其中![]() 是
是![]() 中的最大数,
中的最大数,![]() ,求数列
,求数列![]() 的通项公式.
的通项公式.
在直角坐标平面上有一点列![]() 对一切正整数n,点Pn在函数
对一切正整数n,点Pn在函数![]() 的图象上,且Pn的横坐标构成以
的图象上,且Pn的横坐标构成以![]() 为首项,-1为公差的等差数列{xn}.
为首项,-1为公差的等差数列{xn}.
(1)求点Pn的坐标;
(2)设抛物线列C1,C2,C3,…,Cn,…中的每一条的对称轴都垂直于x轴,抛物线Cn的顶点为Pn,且过点Dn(0,![]() ).记与抛物线Cn相切于点Dn的直线的斜率为kn,求
).记与抛物线Cn相切于点Dn的直线的斜率为kn,求![]()
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com