
题目列表(包括答案和解析)
(理)如图,|AB|=2,O为AB中点,直线 过B且垂直于AB,过A的动直线与
过B且垂直于AB,过A的动直线与 交于点C,点M在线段AC上,满足
交于点C,点M在线段AC上,满足 =
= .
.

(1)求点M的轨迹方程;
(2)若过B点且斜率为-  的直线与轨迹M交于点P,点Q(t,0)是x轴上任意一点,求当ΔBPQ为锐角三角形时t的取值范围.
的直线与轨迹M交于点P,点Q(t,0)是x轴上任意一点,求当ΔBPQ为锐角三角形时t的取值范围.
 如图,几何体SABC的底面是由以AC为直径的半圆O与△ABC组成的平面图形,SO⊥平面ABC,AB⊥BC,SA=SB=SC=A C=4,BC=2.
如图,几何体SABC的底面是由以AC为直径的半圆O与△ABC组成的平面图形,SO⊥平面ABC,AB⊥BC,SA=SB=SC=A C=4,BC=2.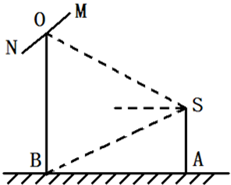 如图,摄影爱好者S在某公园A处,发现正前方B处有一立柱,测得立柱顶端O的仰角和立柱底部B的俯角均为30°,已知S的身高约为
如图,摄影爱好者S在某公园A处,发现正前方B处有一立柱,测得立柱顶端O的仰角和立柱底部B的俯角均为30°,已知S的身高约为| 3 |
| 3 |
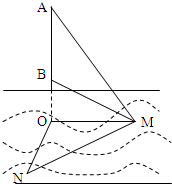 如图,某海域中有甲、乙两艘测量船分别停留在相距(
如图,某海域中有甲、乙两艘测量船分别停留在相距(
 )海里的M,N两地,他们在同时观测岛屿上中国移动信号塔AB,设塔底延长线与海平面交于点O.已知点M在点O的正东方向,点N在点O的南偏西15°方向,ON=
)海里的M,N两地,他们在同时观测岛屿上中国移动信号塔AB,设塔底延长线与海平面交于点O.已知点M在点O的正东方向,点N在点O的南偏西15°方向,ON= 海里,在M处测得塔底B和塔顶A的仰角分别为30°和60°.
海里,在M处测得塔底B和塔顶A的仰角分别为30°和60°.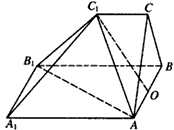
一、选择题(
1.C
2.理D 文D
3.D
4.C. 提示:{f(n)}是等差数列(n∈N*)
5.A. 提示:当S1=S2=S3=S4=S时,λ=4;当高趋向于零时,λ无限接近2
6.A
7.A
8.D
9.B. 提示:∵|PF1|+|PF2|=2,|PF1|-|PF2|=±2,又m-1=n+1,
∴|PF1|2+|PF2|2=2(m+n)=4(m-1)=|F
10.C
11.D
12.D. 提示:第一行C22,第二行C31+C32=C42,第三行C41+C42=C52,…,故S19=C22+C42+C52+…+C122=C133-C32=283.
二、填空题(
13.y=-
14.答案:相反数的相反数是它本身,集合A的补集的补集是它本身,一个复数的共轭的共轭是它本身,等等.
15.nn
16.4或6或7或8
三、解答题
17.解:(1) y=sin2ωx+ cos2ωx+ = sin(2ωx+ )+ (4)
∵ T= ∴ ω =2 (6)
(2) y=sin(4x+ )+
∵ 0≤x≤ ∴ ≤4x+ ≤π + (8)
∴ 当x= 时,y=0 当x=时,y= (12)
18.(1)质点n次移动看作n次独立重复试验,记向左移动一次为事件A,
则P(A)=,P( )=3秒后,质点A在点x=1处的概率P1=P3(1)=C31?p(1-p)2=3××()2=
(
)=3秒后,质点A在点x=1处的概率P1=P3(1)=C31?p(1-p)2=3××()2=
(
(2)2秒后,质点A、B同在x=2处,即A、B两质点各做二次移动,其中质点A向右移动2次,质点B向左、向右各移动一次,故P2=P2(0)?P2(1)=C20?()2?C21??=
(
考点解析:本题考查n次独立重复试验及独立事件同时发生的概率,但需要一定的分析、转化能力.
 |
19.(1)∵AA1⊥面ABCD,∴AA1⊥BD,
又BD⊥AD,∴BD⊥A1D (
又A1D⊥BE,
∴A1D⊥平面BDE
(
(2)连B
∴=,又E为CC1中点,∴BB12=BC2=a2,
∴BB1=a
(
取CD中点M,连BM,则BM⊥平面CD1,作MN⊥DE于N,连NB,则∠BNM是二面角B?DE?C的平面角
(
RtΔCED中,易求得MN=,RtΔBMN中,tan∠BNM==,∴∠BNM=arctan (
(3)易证BN长就是点B到平面A1DE的距离 (
BN==a (
(2)另解:以D为坐标原点,DA为x轴、DB为y轴、DD1为z轴建立空间直角坐标系
则B(0,a,0),设A1(a,0,x),E(-a,a,), =(-a,0,-x),
=(-a,0,-x), =(-a,0,),∵A1D⊥BE
=(-a,0,),∵A1D⊥BE
∴a2-x2=0,x2=
考点解析:九(A)、九(B)合用一道立体几何题是近年立几出题的趋势,相比较而言,选用九(B)体系可以避开一些逻辑论证,取之以代数运算,可以减轻多数学生学习立体几何的学习压力.
20.若按方案1付款,设每次付款为a(万元)
则有a+a(1+0.8%)4+a(1+-0.8%)8=10×(1+0.8%)12 (
即a×=10×1.00812,a=
付款总数S1=
若按方案2付款,设每次付款额为b(万元),同理可得:b= (
付款总额为S2=12b=9.6×1.00812,故按有二种方案付款总额较少. (
考点解析:复习中要注意以教材中研究性学习内容为背景的应用问题.
 21.(理)(1)设M(x,y),C(1,y0),∵=,∴=
(
21.(理)(1)设M(x,y),C(1,y0),∵=,∴=
(
又A、M、C三点一线,∴= ②
(
由(1)、(2)消去y0,得x2+4y2=1(y≠0)
(
(2)P(0,)是轨迹M短轴端点,∴t≥0时∠PQB或∠PBQ不为锐角,∴t<0
又∠QPB为锐角,∴ ?
? >0,∴(t,- )(1,- )=t+ >0,∴- <t<0
(
>0,∴(t,- )(1,- )=t+ >0,∴- <t<0
(
考点解析:解析几何题注意隐藏的三点共线关系;平面向量运算也常常设置在解析几何考题当中.
21.(文)证明:(1) 设-1<x1<x2<+∞
f(x1)-f(x2) =a-a + -
=a-a + (4)
∵ -1<x1<x2 ,a>0
∴ a-a<0 <0
∴ f(x1)-f(x2)<0 即 f(x1)<f(x2) ,函数f(x)在(-1,+∞ )上为增函数. (6)
(2) 若方程有负根x0 (x0≠-1),则有a= -1
若 x0<-1 , -1<-1 而 a>0 故 a ≠ -1 (10)
若 -1<x0<0 , -1>2 而 a<a0=
综上所述,方程f(x)=0没有负根.
(12)
22.(理)(1)Sn=an,∴Sn+1=an+1,an+1=Sn+1-Sn=an+1-an,∴= (n≥2)
(
∴==…==1,∴an+1=n,an=n-1 (n≥2),又a1=0,∴an=n-1
(
(2)bn+1=(1+ )n+1,bn=(1+ )n,
∵<(n+1)?(1+ )n
(
整理即得:(1+ )n<(1+ )n+1,即bn<bn+1
(
(3)由(2)知bn>bn-1>…>b1=
(
又Cnr?()r=(??…)?()r≤()r,(0≤r≤n),
∴bn≤1+ +()2+…+()n=2-()n<2,∴≤bn<2
(
考点解析:这种“新概念”题需要较好的理解、分析能力,放缩法证明不等式是不等式证明的常用方法,也具有一定的灵活性,平时要注重概念的学习,常见题型的积累,提高思维能力和联想变通能力.
22.(文)见21(理).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com