
题目列表(包括答案和解析)
两根相距d=0.20 m的平行金属长导轨固定在同一水平面内,并处于竖直方向的匀强磁场中,磁场的磁感应强度B=0.20 T,导轨上面横放着两条金属细杆,构成矩形闭合回路.每条金属细杆的电阻为r=0.25 Ω,回路中其余部分的电阻可不计,已知两金属细杆在平行导轨的拉力作用下沿导轨朝相反方向匀速平移,速度大小都是v=5.0 m/s,如图所示,不计导轨上的摩擦.
(1)求作用于每条金属细杆的拉力的大小.
(2)求两金属细杆在间距增加0.40 m的滑动过程中共产生的热量.
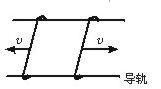
两根相距d=0.20 m的平行金属长导轨固定在同一水平面内,并处于竖直方向的匀强磁场中,磁场的磁感应强度B=0.20 T,导轨上面横放着两条金属细杆,构成矩形闭合回路.每条金属细杆的电阻为r=0.25 Ω,回路中其余部分的电阻可不计,已知两金属细杆在平行导轨的拉力作用下沿导轨朝相反方向匀速平移,速度大小都是v=5.0 m/s,如图所示,不计导轨上的摩擦.
(1)求作用于每条金属细杆的拉力的大小.
(2)求两金属细杆在间距增加0.40 m的滑动过程中共产生的热量.
两根相距d="0.20" m的平行金属长导轨固定在同一水平面内,并处于竖直方向的匀强磁场中,磁场的磁感应强度B="0.20" T,导轨上面横放着两条金属细杆,构成矩形闭合回路.每条金属细杆的电阻为r="0.25" Ω,回路中其余部分的电阻可不计,已知两金属细杆在平行导轨的拉力作用下沿导轨朝相反方向匀速平移,速度大小都是v="5.0" m/s,如图所示,不计导轨上的摩 擦.
擦.
(1)求作用于每条金属细杆的拉力的大小.
(2)求两金属细杆在间距增加0.40 m的滑动过程中共产生的热量 .
.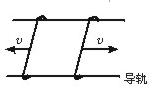
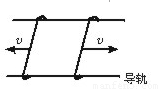
两根相距d=0.20 m的平行金属长导轨固定在同一水平面内,并处于竖直方向的匀强磁场中,磁场的磁感应强度B=0.20 T,导轨上面横放着两条金属细杆,构成矩形闭合回路.每条金属细杆的电阻为r=0.25 Ω,回路中其余部分的电阻可不计,已知两金属细杆在平行导轨的拉力作用下沿导轨朝相反方向匀速平移,速度大小都是v=5.0 m/s,如图所示,不计导轨上的摩擦.
(1)求作用于每条金属细杆的拉力的大小.
(2)求两金属细杆在间距增加0.40 m的滑动过程中共产生的热量.
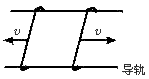
 1.B.提示:将圆环转换为并联电源模型,如图
1.B.提示:将圆环转换为并联电源模型,如图
2.CD 3.AD
4.Q=IΔt= 或Q=
或Q=
5.(1)3.2×10-2 N (2)1.28×10-2 J
提示:将电路转换为直流电路模型如图. 
6.(1)电压表 理由略
(2)F=1.6 N (3)Q=
7.(1)如图所示,当EF从距BD端s处由静止开始滑至BD的过程中,受力情况如图所示.安培力:F安=BIl=B

根据牛顿第二定律:a= ①
①
所以,EF由静止开始做加速度减小的变加速运动.当a=0时速度达到最大值vm.
由①式中a=0有:Mgsinθ-B
vm=
(2)由恒力F推至距BD端s处,棒先减速至零,然后从静止下滑,在滑回BD之前已达最大速度vm开始匀速.
设EF棒由BD从静止出发到再返回BD过程中,转化成的内能为ΔE.根据能的转化与守恒定律:
Fs-ΔE= Mvm2 ③
Mvm2 ③
ΔE=Fs- M(
M( )2 ④
)2 ④
8.(1)每半根导体棒产生的感应电动势为
E1=Bl =
= Bl2ω=
Bl2ω= ×0.4×103×(0.5)2 V=50 V.
×0.4×103×(0.5)2 V=50 V.
(2)两根棒一起转动时,每半根棒中产生的感应电动势大小相同、方向相同(从边缘指向中心),相当于四个电动势和内阻相同的电池并联,得总的电动势和内电阻
为E=E1=50 V,r= R0=0.1 Ω
R0=0.1 Ω
当电键S断开时,外电路开路,电流表示数为零,电压表示数等于电源电动势,为50 V.
当电键S′接通时,全电路总电阻为
R′=r+R=(0.1+3.9)Ω=4Ω.
由全电路欧姆定律得电流强度(即电流表示数)为
I= A=
A=
此时电压表示数即路端电压为
U=E-Ir=50-12.5×0.1 V=48.75 V(电压表示数)
或U=IR=12.5×3.9 V=48.75 V
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com