
题目列表(包括答案和解析)
 (2007•浦东新区二模)已知抛物线C:y2=2px(p>0)上横坐标为4的点到焦点的距离为5.
(2007•浦东新区二模)已知抛物线C:y2=2px(p>0)上横坐标为4的点到焦点的距离为5.| 16(1-kb) | k2 |
(本小题满分12分)
某校共有800名学生,高三一次月考之后,为了了解学生学习情况,用分层抽样方法从中抽出若干学生此次数学成绩,按成绩分组,制成如下的频率分布表:
|
组号 |
第 一 组 |
第 二 组 |
第 三 组 |
第 四 组 |
第 五 组 |
第 六 组 |
第 七 组 |
第 八 组 |
合计 |
|
分组 |
|
|
|
|
|
|
|
|
|
|
频数 |
4 |
6 |
20 |
22 |
18 |
|
10 |
5 |
|
|
频率 |
0.04 |
0.06 |
0.20 |
0.22 |
|
0.15 |
0.10 |
0.05 |
1 |
(Ⅰ) 李明同学本次数学成绩为103分,求他被抽中的概率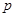 ;
;
(Ⅱ) 为了了解数学成绩在120分以上的学生的心理状态,现决定在第六、七、八组中用分层抽样方法抽取6名学生的成绩,并在这6名学生中在随机抽取2名由心理老师张老师负责面谈,求第七组至少有一名学生与张老师面谈的概率;
(Ⅲ) 估计该校本次考试的数学平均分。
(本小题满分12分)
某校共有800名学生,高三一次月考之后,为了了解学生学习情况,用分层抽样方法从中抽出若干学生此次数学成绩,按成绩分组,制成如下的频率分布表:
| 组号 | 第 一 组 | 第 二 组 | 第 三 组 | 第 四 组 | 第 五 组 | 第 六 组 | 第 七 组 | 第 八 组 | 合计 |
| 分组 | 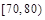 | 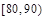 | 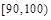 | 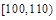 | 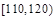 | 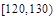 |  | 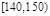 | |
| 频数 | 4 | 6 | 20 | 22 | 18 | 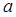 | 10 | 5 | 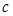 |
| 频率 | 0.04 | 0.06 | 0.20 | 0.22 | 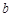 | 0.15 | 0.10 | 0.05 | 1 |
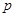 ;
;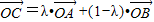 成立,此时称实数λ为“向量
成立,此时称实数λ为“向量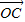 关于
关于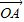 和
和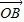 的终点共线分解系数”.若已知P1(3,1)、P2(-1,3),且向量
的终点共线分解系数”.若已知P1(3,1)、P2(-1,3),且向量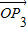 是直线l:x-y+10=0的法向量,则“向量
是直线l:x-y+10=0的法向量,则“向量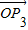 关于
关于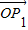 和
和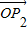 的终点共线分解系数”为 .
的终点共线分解系数”为 .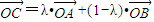 成立,此时称实数λ为“向量
成立,此时称实数λ为“向量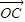 关于
关于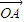 和
和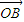 的终点共线分解系数”.若已知P1(3,1)、P2(-1,3),且向量
的终点共线分解系数”.若已知P1(3,1)、P2(-1,3),且向量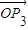 是直线l:x-y+10=0的法向量,则“向量
是直线l:x-y+10=0的法向量,则“向量 关于
关于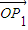 和
和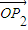 的终点共线分解系数”为 .
的终点共线分解系数”为 .湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com