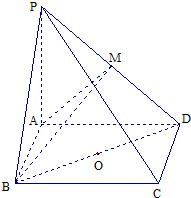如图，在四棱锥P-ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA=AD=4，AB=2，以BD的中点O为球心、BD为直径的球面交PD于点M，
（1）求证：平面ABM⊥平面PCD；
（2）求直线PC与平面ABM所成的角；
（3）求点O到平面ABM的距离．

查看答案和解析>>

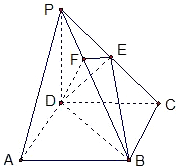如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC，E是PC的中点，作EF⊥PB交PB于点F．
（1）证明PA∥平面EDB；
（2）证明PB⊥平面EFD；
（3）求二面角C-PB-D的大小．

查看答案和解析>>

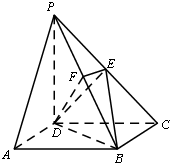如图，在四棱锥P-ABCD中，底面ABCD是矩形，侧棱PD⊥底面ABCD，PD=DC，E是PC的中点，作EF⊥PB交PB于点F．
（1）证明：PA∥平面EDB；
（2）证明：PB⊥平面EFD．
（3）若AB=4，BC=3，求点C到平面PBD的距离．

查看答案和解析>>

如图，在四棱锥P-ABCD中，底面ABCD是矩形，M、N分别为PA、BC的中点，PD⊥平面ABCD，且PD=AD=

2

，CD=1．
（1）证明：MN∥平面PCD；
（2）证明：MC⊥BD；
（3）求二面角A-PB-D的余弦值．

查看答案和解析>>

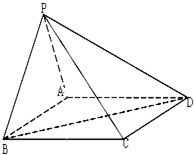如图，在四棱锥P-ABCD中，底面ABCD是矩形．已知AB=3，AD=2，PA=2，PD=2

2

，∠PAB=60°．
（Ⅰ）证明AD⊥平面PAB；
（Ⅱ）求异面直线PC与AD所成的角的大小；
（Ⅲ）求二面角P-BD-A的大小．

查看答案和解析>>

2009年4月

一、选择题：本大题共10小题，每题5分，共50分．

1．B    2．A    3．C    4．C    5．B    6．A    7．C    8．A    9．B   10．B

二、填空题：本大题共5小题，每题5分，共25分．

11．4                                      12．                                  13．

14．                                  15．①

三、解答题：本题共6小题，共75分．

16．解：(1)  

∴

∵

∴  

∴

(2)  

∴        

∴  

∴  

∴  

17．解：(1) 甲队以二比一获胜，即前两场中甲胜1场，第三场甲获胜，其概率为

(2) 乙队以2∶0获胜的概率为；

乙队以2∶１获胜的概率为

∴乙队获胜的概率为P₂=P'₂+Ｐ''₂=0.16+0.192=0.352.

18．解：(1) ∵  函数是定义在R上的奇函数，

∴

∵       ∴  ．

又在处的切线方程为，

由

∴  ，且， ∴  得

(2)

依题意对任意恒成立，   

∴ 对任意恒成立，即对任意恒成立，

∴ ．

19．解法一：(1) 证明：取中点为，连结、，

               ∵△是等边三角形， ∴

               又∵侧面底面，

               ∴底面，

               ∴为在底面上的射影，

               又∵，

               ，

               ∴，  ∴，

                ∴，      ∴．

(2) 取中点，连结、，    

    ∵．    ∴．

又∵，，

∴平面，∴，

∴是二面角的平面角.                  

∵，，

∴．

∴，∴，∴，

∴二面角的大小为                       

解法二：证明：(1) 取中点为，中点为，连结，

∵△是等边三角形，∴，

又∵侧面底面，∴底面，

∴以为坐标原点，建立空间直角坐标系

如图，   

∵，△是等边三角形，

∴，

∴．

∴．

∵     ∴．

(2) 设平面的法向量为

∵   ∴

令，则，∴               

设平面的法向量为，              

∵，∴，

令，则，∴       

∴，

∴，   ∴二面角的大小为.        

20．解：(1) 由题意得，  ①， 

当时，，解得，

当时，有  ②，

①式减去②式得，

于是，，，

因为，所以，

所以数列是首项为，公差为的等差数列，

所以的通项公式为（）．

(2) 设存在满足条件的正整数，则，，，

又，，…，，，，…，，

所以，，…，均满足条件，

它们组成首项为，公差为的等差数列．……（8分）

设共有个满足条件的正整数，则，解得．（10分）

所以，中满足条件的正整数存在，共有个，的最小值为．（12分）

21．（Ⅰ）法1：依题意，显然的斜率存在,可设直线的方程为

，

整理得 ． ①

设是方程①的两个不同的根，

∴，   ②

且，由是线段的中点，得

，∴．

解得，代入②得，的取值范围是（12，+∞）．

于是，直线的方程为，即   

法2：设，，则有

依题意，，∴．

∵是的中点，∴，，从而．

又由在椭圆内，∴，

∴的取值范围是．    

直线的方程为，即．   

(2)  ∵垂直平分，∴直线的方程为，即，

代入椭圆方程，整理得．  ③      

又设，的中点为，则是方程③的两根，

∴．

到直线的距离，

故所求的以线段的中点为圆心且与直线相切的圆的方程为：

．