练习册

  • 练习册
  • 试题
    18． 某大学宿舍共有7个同学.其中4个同学从来没有参加过社会实践活动.3个同学曾经参加过社会实践活动．(Ⅰ)现从该宿舍中任选2个同学参加一项社会实践活动.求恰好选到1个曾经参加过社会实践活动的同学的概率,(Ⅱ)若从该宿舍中任选2个同学参加社会实践活动.求活动结束后.该宿舍至少有3个同学仍然没有参加过社会实践活动的概率． 【查看更多】

     

    题目列表(包括答案和解析)

    （本小题满分12分）

        某大学毕业生参加一个公司的招聘考试，考试分笔试和面试两个环节，笔试有A、B两个题目，该学生答对A、B两题的概率分别为、，两题全部答对方可进入面试.面试要回答甲、乙两个问题，该学生答对这两个问题的概率均为，至少答对一题即可被聘用（假设每个环节的每个问题回答正确与否是相互独立的）.

       （I）求该学生被公司聘用的概率；

       （II）设该学生答对题目的个数为，求的分布列和数学期望.

     

    查看答案和解析>>

    （本小题满分12分）

    某项选拔共有三轮考核，每轮设有一个问题，能正确回答问题者进入下一轮考试，否则即被淘汰，已知某选手能正确回答第一、二、三轮的问题的概率分别为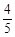、、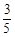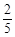，且各轮问题能否正确回答互不影响.

    （Ⅰ）求该选手被淘汰的概率；

    （Ⅱ）该选手在选拔中回答问题的个数记为ξ，求随机变量ξ的分布列与数数期望.（注：本小题结果可用分数表示）

     

    查看答案和解析>>

    （本小题满分12分）

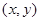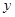    某市地铁全线共有四个车站，甲、乙两人同时在地铁第一号车站(首发站)乘车.假设每人自第2号车站开始,在每个车站下车是等可能的。约定用有序实数对表示“甲在号车站下车，乙在号车站下车”．

    （1）用有序实数对把甲、乙两人下车的所有可能的结果列举出来；

    （2）求甲、乙两人同在第3号车站下车的概率；

    （3）求甲、乙两人在不同的车站下车的概率．

     

    查看答案和解析>>

    （本小题满分12分）

    某大学高等数学老师上学期分别采用了两种不同的教学方式对甲、乙两个大一新生班进行教改试验（两个班人数均为60人，入学数学平均分数和优秀率都相同；勤奋程度和自觉性都一样）。现随机抽取甲、乙两班各20名同学的上学期数学期末考试成绩，得到茎叶图如下：

    （Ⅰ）依茎叶图判断哪个班的平均分高？

    （Ⅱ）从乙班这20名同学中随机抽取两名高等数学成绩不得低于85分的同学，求成绩为90分的同学被抽中的概率；

    （Ⅲ）学校规定：成绩不低于85分的为优秀，请填写下面的列联表，并判断“能否在犯错误的概率不超过0.025的前提下认为成绩优秀与教学方式有关？”

     

    甲班

    乙班

    合计

    优秀

     

     

     

    不优秀

     

     

     

    合计

     

     

     

    下面临界值表仅供参考：

    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    2.072

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    （参考公式：其中） 

    （Ⅳ）从乙班高等数学成绩不低于85分的同学中抽取2人，成绩不低于90分的同学得奖金100元，否则得奖金50元，记为这2人所得的总奖金，求的分布列和数学期望。

     

    查看答案和解析>>

    （本小题满分12分）

        某旅游公司为3个旅游团提供甲、乙、丙、丁4条旅游线路，每个旅游团从中任选一条。

       （I）求3个旅游团选择3条不同的旅游线路的概率；

       （II）求恰有2条旅游线路没有被选择的概率；

       （III）求选择甲旅游线路的旅游团数的分布列及数学期望。

     

    查看答案和解析>>

    评分说明：

    1．本解答给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分参考制订相应的评分细则．

    2．对计算题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的内容和难度，可视影响的程度决定后继部分的给分，但不得超过该部分正确解答应得分数的一半；如果后继部分的解答有较严重的错误，就不再给分．

    3．解答右端所注分数，表示考生正确做到这一步应得的累加分数．

    4．只给整数分数．选择题不给中间分．

    一．选择题

    1．D      2．B       3．B       4．C       5．A      6．C       7．C       8．A      9．B       10．D

    11．B     12．D

    二．填空题

    13．300；     14．60；       15．①、②③或①、③②；     16．103．

    三．解答题

    17．解：

    （Ⅰ）因为点的坐标为，根据三角函数定义可知，，，

    所以．     2分

    （Ⅱ）∵，，∴． 3分

    由余弦定理，得 

    ．   5分

    ∵，∴，∴． 7分

    ∴，∴．     9分

    故BC的取值范围是．（或写成） 10分

    18．解：

    （Ⅰ）记“恰好选到1个曾经参加过社会实践活动的同学”为事件的，    1分

    则其概率为．   5分

    （Ⅱ）记“活动结束后该宿舍至少有3个同学仍然没有参加过社会实践活动”为事件的B，“活动结束后该宿舍仍然有3个同学没有参加过社会实践活动”为事件的C，“活动结束后该宿舍仍然有4个同学没有参加过社会实践活动”为事件的D． 6分

    ∵，．     10分

    =+=．      12分

    19．证：

    （Ⅰ）因为四边形是矩形∴，

    又∵AB⊥BC，∴平面．     2分

    ∵平面，∴平面CA1B⊥平面A1ABB1．       3分

    解：（Ⅱ）过A1作A1D⊥B1B于D，连接，

    ∵平面，

    ∴BC⊥A1D．

    ∴平面BCC1B1，

    故∠A1CD为直线与平面所成的角．

           5分

    在矩形中，，

    因为四边形是菱形，∠A1AB＝60°, CB＝3，AB＝4，

    ，． 7分

    （Ⅲ）∵，∴平面．

    ∴到平面的距离即为到平面的距离． 9分

    连结，与交于点O，

    ∵四边形是菱形，∴．

    ∵平面平面，∴平面．

    ∴即为到平面的距离． 11分

    ，∴到平面的距离为．  12分

     

    20．解：

    （Ⅰ）由题意，，  1分

    又∵数列为等差数列，且，∴．   3分

    ∵，∴．     5分

    （Ⅱ）的前几项依次为， 7分

    ∴＝5．    8分

    ∴＝．    12分

    21．解：

    （Ⅰ）∵，     2分

    由，得或．     4分

    的单调增区间为和．  5分

    （Ⅱ）当时，恒有||≤2，即恒有成立．

    即当时，      6分

    由（Ⅰ）知在上为增函数，在上为减函数，在上为增函数，

    ∵，，∴．

    ∴max＝．       8分

    ∵，，∴．

    ∴min＝．   10分

    由且．解得．

    所以，当时，函数在上恒有||≤2成立． 12分

    22．解：

    （Ⅰ）由已知，，

    由解得    2分

    ∵，∴

    轴，．  4分

    ∴，

    ∴成等比数列．    6分

    （Ⅱ）设、，由

    消得  ，

    ∴   8分

    ∵

    ．     10分

    ∵，∴．∴，或．

    ∵m>0，∴存在，使得．     12分

     


    同步练习册答案