
题目列表(包括答案和解析)
已知二次函数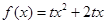

(Ⅰ)求不等式 的解集;
的解集;
(Ⅱ)若 ,记
,记 为数列
为数列 的前
的前 项和,且
项和,且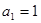 ,
,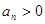
 ),点
),点 在函数
在函数 的图像上,求
的图像上,求 的表达式.
的表达式.
(本小题满分14分)
在![]() 平面上有一系列的点
平面上有一系列的点![]() , 对于正整数
, 对于正整数![]() ,点
,点![]() 位于函数
位于函数![]() 的图像上,以点
的图像上,以点![]() 为圆心的
为圆心的![]() 与
与![]() 轴相切,且
轴相切,且![]() 与
与![]() 又彼此外切,若
又彼此外切,若![]() ,且
,且![]()
(1)求证:数列![]() 是等差数列;
是等差数列;
(2)设![]() 的面积为
的面积为![]() ,
,![]() 求证:
求证:![]()
已知函数y=f(x)是定义在区间[- ,
, ]上的偶函数,且
]上的偶函数,且
x∈[0, ]时,
]时,
(1)求函数f(x)的解析式;
(2)若矩形ABCD的顶点A,B在函数y=f(x)的图像上,顶点C,D在x轴上,求矩形ABCD面积的最大值.
为了得到函数![]() 的图像,只需把函数
的图像,只需把函数![]() 的图像上所有的点 ( )
的图像上所有的点 ( )
A.向左平移3个单位长度,再向上平移1个单位长度
B.向右平移3个单位长度,再向上平移1个单位长度
C.向左平移3个单位长度,再向下平移1个单位长度
D.向右平移3个单位长度,再向下平移1个单位长度
等比数列{![]() }的前n项和为
}的前n项和为![]() , 已知对任意的
, 已知对任意的![]() ,点
,点![]() ,均在函数
,均在函数![]() 且
且![]() 均为常数)的图像上.
均为常数)的图像上. ![]()
![]()
(1)求r的值;
(11)当b=2时,记 ![]() 求数列
求数列![]() 的前
的前![]() 项和
项和![]()
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com