
题目列表(包括答案和解析)
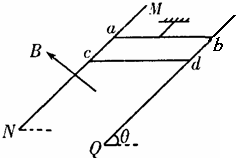 如图所示,MN、PQ是与水平面成θ角的两条平行光滑且足够长的金属导轨,其电阻忽略不计.空间存在着垂直于轨道平面向上的匀强磁场,磁感应强度大小为B.导体棒ab、cd垂直于导轨放置,且与轨道接触良好,每根导体棒的质量均为m,电阻均为r,轨道宽度为L.与导轨平行的绝缘细线一端固定,另一端与ab棒中点连接,细线承受的最大拉力Tm=2mgsinθ.今将cd棒由静止释放,则细线被拉断时,cd棒的( )
如图所示,MN、PQ是与水平面成θ角的两条平行光滑且足够长的金属导轨,其电阻忽略不计.空间存在着垂直于轨道平面向上的匀强磁场,磁感应强度大小为B.导体棒ab、cd垂直于导轨放置,且与轨道接触良好,每根导体棒的质量均为m,电阻均为r,轨道宽度为L.与导轨平行的绝缘细线一端固定,另一端与ab棒中点连接,细线承受的最大拉力Tm=2mgsinθ.今将cd棒由静止释放,则细线被拉断时,cd棒的( )A、速度大小是
| ||
B、速度大小是
| ||
| C、加速度大小是2gsinθ | ||
| D、加速度大小是0 |
如图所示,MN、PQ是与水平面成θ角的两条平行光滑且足够长的金属导轨,其电阻忽略不计。空间存在着垂直于轨道平面向上的匀强磁场,磁感应强度大小为B。导体棒ab、cd垂直于导轨放置,且与轨道接触良好,每根导体棒的质量均为m,电阻均为r,轨道宽度为L。与导轨平行的绝缘细线一端固定,另一端与ab棒中点连接,细线承受的最大拉力Tm=2mgsinθ。今将cd棒由静止释放,则细线被拉断时,cd棒的 ( )
A.速度大小是![]()
B.速度大小是![]()
C.加速度大小是![]()
D.加速度大小是0
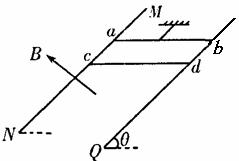
A.速度大小是
| ||
B.速度大小是
| ||
| C.加速度大小是2gsinθ | ||
| D.加速度大小是0 |

A.速度大小是![]()

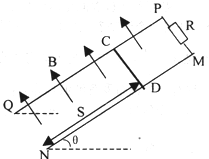 如图所示,MN、PQ是两根足够长的平行光滑导轨,两导轨间距为L,导轨平面与水平面的夹角为θ,两导轨间垂直于导轨平面有斜向上的匀强磁场,磁感应强度为B,导轨MP端连有一阻值为R的电阻,其余电阻不计.若将一垂直于导轨,质量为M的金属棒CD在距NQ端为S处由静止释放,则CD棒滑至底端前,会经历加速运动和匀速运动两个阶段.今用大小为F,方向沿斜面向上的恒力把CD棒从NQ由静止开始推至距NQ端为S处,撤去恒力F,棒CD最后又回到NQ端.
如图所示,MN、PQ是两根足够长的平行光滑导轨,两导轨间距为L,导轨平面与水平面的夹角为θ,两导轨间垂直于导轨平面有斜向上的匀强磁场,磁感应强度为B,导轨MP端连有一阻值为R的电阻,其余电阻不计.若将一垂直于导轨,质量为M的金属棒CD在距NQ端为S处由静止释放,则CD棒滑至底端前,会经历加速运动和匀速运动两个阶段.今用大小为F,方向沿斜面向上的恒力把CD棒从NQ由静止开始推至距NQ端为S处,撤去恒力F,棒CD最后又回到NQ端.14.C 15.C 16.A 17.B 18.AD 19.D 20.AD 21.BC
22.(1)①保证小球沿水平方向抛出② ③1.0,1.5
③1.0,1.5
(2)甲图不合理之处:不能多次测量;超过电流表量程,不安全;超过电压表量程,也不安全。郝 双制 作
乙图不合理之处:电流表量程太小;电压表量程太大。
较为合理的电路如图所示,

Rx的计算公式 ,其中U是电压表V1示数,I是电流表A1示数,R0是电阻箱示数。
,其中U是电压表V1示数,I是电流表A1示数,R0是电阻箱示数。
23. 解:滑块从A处到B处,由动能定理mgssin37°-μmgscos37°= mvB2
mvB2
滑块从B到C处,由动能定理-μmgBC= mvC2-
mvC2- mvB2
mvB2
若滑块恰好从C处平抛射出,则在C处时不受弹力作用 mg=m
联立解得郝双 BC=
所以水平滑槽BC长度至少为
24. 解:⑴设第1个球与木盒相遇后瞬间,两者共同运动的速度为v1,根据动量守恒定律:
 代入数据,解得: v1=
代入数据,解得: v1=
⑵设第1个球与木盒的相遇点离传送带左端的距离为s,第1个球经过t0与木盒相遇,
则: 
设第1个球进入木盒后两者共同运动的加速度为a,根据牛顿第二定律:
 得:
得: 
设木盒减速运动的时间为t1,加速到与传送带相同的速度的时间为t2,则:

故木盒在2s内的位移为零
依题意: 
代入数据,解得:郝双 
25.解:(1)小球进入电场,做匀速直线运动时 Eq=mg ①E=mg/q②
(2)在t1时刻加磁场,小球在时间t0内做匀速圆周运动,设圆周运动周期为T0,半径为R。
竖直向下通过D点,则t0=3T0/4③  ④
④
PF-PD=R即 ⑤
⑤
将③、④代入⑤式解得 ⑥
⑥

(3)小球运动的速率始终不变,当R变大时,T0也增加,小球在电场中的运动周期T也增加。
在小球不飞出电场的情况下,当T最大时,有:郝双 制作
DQ=2R即 ⑥
⑥  ⑦
⑦
结合⑥⑦式解得 ⑧
⑧
 ⑨
⑨
结合轨迹图可知,小球在电场中运动的最大周期 ⑩
⑩
结合上式解得
小球在电场中运动一个周期的轨迹图如图乙所示
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com