
题目列表(包括答案和解析)
设函数f(x)=![]() +sinx的所有正的极小值点从小到大排成的数列为{xn}.
+sinx的所有正的极小值点从小到大排成的数列为{xn}.
(Ⅰ)求数列{xn}的通项公式;
(Ⅱ)设{xn}的前n项和为Sn,求sinSn.
已知函数
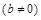 在
在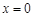 处取到极值2.
处取到极值2.
(Ⅰ)求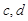 的值;
的值;
(Ⅱ)试研究曲线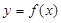 的所有切线与直线
的所有切线与直线 垂直的条数;
垂直的条数;
(Ⅲ)若对任意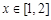 ,均存在
,均存在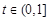 ,使得
,使得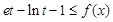 ,试求
,试求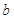 的取值范围.
的取值范围.
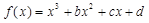
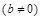 在
在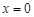 处取到极值2.
处取到极值2.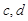 的值;
的值;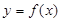 的所有切线与直线
的所有切线与直线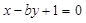 垂直的条数;
垂直的条数;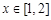 ,均存在
,均存在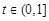 ,使得
,使得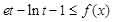 ,试求
,试求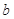 的取值范围.
的取值范围. 已知定义在![]() 上的奇函数
上的奇函数![]() 的导函数为
的导函数为![]() ,且
,且![]() 在点
在点![]() 处取得极值.
处取得极值.
(1)求函数![]() 的解析式;
的解析式;
(2)若函数![]() 在区间
在区间![]() 上是增函数,求实数
上是增函数,求实数![]() 所有取值的集合;
所有取值的集合;
(3)当![]() 时,求
时,求![]() 的最大值.
的最大值.
(理 )如图,正三棱柱
)如图,正三棱柱 的所有棱长都为
的所有棱长都为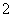 ,
, 为
为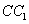 中点.
中点.
(Ⅰ)求证: 平面
平面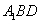 ;
;
(Ⅱ)求二面角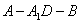 的大小;
的大小;
(Ⅲ)求点 到平面
到平面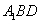 的距离.
的距离.
(文)设函数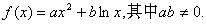
证明:当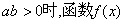 没有极值点;当
没有极值点;当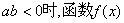 有且只有一个极值点,并求出极值
有且只有一个极值点,并求出极值
一、选择题
1~4 BBCA 5~8 ADCD
二、填空题
9、 10、
10、  =
= 11、
11、  12. 42
;
12. 42
; 
13. 2或 14.
14. 15.
15. 
三、解答题
16(本小题满分12分)
1)
 ………………4分
………………4分
2)当 单调递减,故所求区间为
单调递减,故所求区间为 ………………8分
………………8分
(3) 时
时
 ………………12分
………………12分
17(本题满分14分)
解:(Ⅰ)由函数 的图象关于原点对称,得
的图象关于原点对称,得 ,………1分
,………1分
∴ ,∴
,∴ . ………2分
. ………2分
∴ ,∴
,∴ . ……………3分
. ……………3分
∴ ,即
,即 . ………………5分
. ………………5分
∴ . ……………………………6分
. ……………………………6分
(Ⅱ)由(Ⅰ)知 ,∴
,∴ .
.
由 ,∴
,∴ . …………………8分
. …………………8分








0
+
0


ㄋ
极小
ㄊ
极大
ㄋ
∴ . …………12分
. …………12分
18
证明:(I)在正 中,
中, 是
是 的中点,所以
的中点,所以 .
.
又 ,
, ,
, ,所以
,所以 .
.
而 ,所以
,所以 .所以由
.所以由 ,有
,有 .
.
(II)取正 的底边
的底边 的中点
的中点 ,连接
,连接 ,则
,则 .
.
 又
又 ,所以
,所以 .
.
如图,以点 为坐标原点,
为坐标原点, 为
为 轴,
轴, 为
为 轴,
轴,
建立空间直角坐标系.设 ,则有
,则有 ,
,
 ,
, ,
, ,
, ,
, ,
, .再设
.再设 是面
是面 的法向量,则有
的法向量,则有
 ,即
,即 ,可设
,可设 .
.
又 是面
是面 的法向量,因此
的法向量,因此
 ,
,
所以 ,即平面PAB与平面PDC所成二面角为
,即平面PAB与平面PDC所成二面角为 .
.
(Ⅲ)由(II)知 ,设
,设 与面
与面 所成角为
所成角为 ,则
,则
 所以
所以 与面
与面 所成角的正弦值为
所成角的正弦值为 .
.
19(本题满分14分)

20解:(I)建立图示的坐标系,设椭圆方程为 依题意,
依题意,


椭圆方程为 ………………………………2分
………………………………2分
F(-1,0)将x=-1代入椭圆方程得
∴当彗星位于太阳正上方时,二者在图中的距离为1.5┩.……………………6分
(Ⅱ)由(I)知,A1(-2,0),A2(2,0),
|