
题目列表(包括答案和解析)
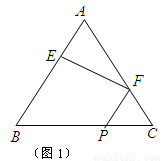
在正三角形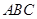 中,
中,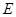 、
、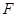 、
、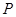 分别是
分别是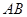 、
、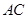 、
、 边上的点,满足
边上的点,满足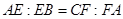
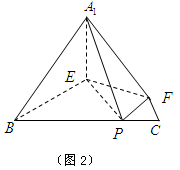
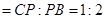 (如图1).将△
(如图1).将△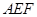 沿
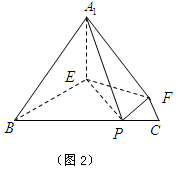
沿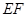 折起到
折起到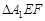 的位置,使二面角
的位置,使二面角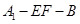 成直二面角,连结
成直二面角,连结 、
、 (如图2)
(如图2)

(Ⅰ)求证: ⊥平面
⊥平面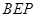 ;
;
(Ⅱ)求二面角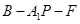 的余弦值.
的余弦值.
在正三角形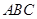 中,
中,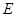 、
、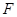 、
、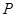 分别是
分别是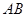 、
、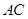 、
、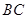 边上的点,满足
边上的点,满足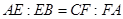
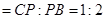 (如图1).将△
(如图1).将△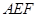 沿
沿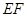 折起到
折起到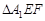 的位置,使二面角
的位置,使二面角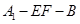 成直二面角,连结
成直二面角,连结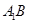 、
、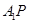 (如图2)
(如图2)
(Ⅰ)求证: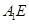 ⊥平面
⊥平面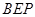 ;
;
(Ⅱ)求二面角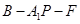 的余弦值.
的余弦值.
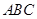 中,
中,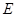 、
、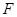 、
、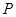 分别是
分别是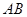 、
、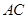 、
、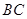 边上的点,满足
边上的点,满足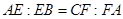
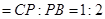 (如图1).将△
(如图1).将△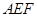 沿
沿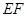 折起到
折起到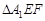 的位置,使二面角
的位置,使二面角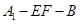 成直二面角,连结
成直二面角,连结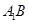 、
、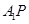 (如图2)
(如图2)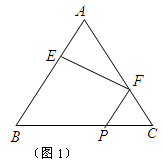
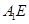 ⊥平面
⊥平面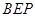 ;
;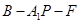 的余弦值.
的余弦值.如图,在正三角形ABC中,D、E、F分别为各边上的中点,G、H、I、J分别为AF、AD、DE、DB上的中点.将△ABC沿DE、EF、DF折成三棱锥后,GH与IJ所成的角的度数是
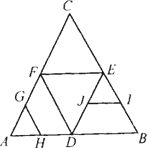
A.90°
B.60°
C.30°
D.0°
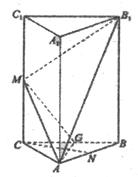
如图,在正三棱柱ABC-A1B1C1中,底面ABC为正三角形,M、N、G分别是棱CC1、AB、BC的中点,且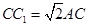 .
.
(Ⅰ)求证:CN∥平面AMB1;
(Ⅱ)求证: B1M⊥平面AMG.
一、选择题:1、A2、A3、B4、B5、C6、D7、B8、D9、D10、A
二、填空题:11、1000
12、 13、三条侧棱
13、三条侧棱 、
、 、
、 两两互相垂直的三棱锥
两两互相垂直的三棱锥 中,
中, ,则此三棱锥的外接球半径为
,则此三棱锥的外接球半径为 14、(1)8 (2)
14、(1)8 (2)
三、解答题:
15、(1)∵ , ∴
, ∴ ,
………(2分)
,
………(2分)
∴ ,( 4分)
,( 4分) ,………(6分)
,………(6分)
∴ 或
或
所求解集为 ………(8分)
………(8分)
(2)∵
∴ ………(10分)
………(10分)
∴ ………(12分)
………(12分)

求 的周期为
的周期为 ,
,
递增区间
16、解:解析:由题意可知,这个几何体是直三棱柱,且 ,
, ,
,
(1)连结 ,
, 。
。
由直三棱柱的性质得 平面
平面 ,所以
,所以 ,则
,则
四边形 为矩形.
为矩形.
由矩形性质得, 过
过 的中点
的中点
在 中,由中位线性质,得
中,由中位线性质,得 ,
,
又 平面
平面 ,
, 平面
平面 ,
,
所以 平面
平面 。 (6分)
。 (6分)
(2)因为 平面
平面 ,
, 平面
平面 ,所以
,所以 ,
,
在正方形 :中,
:中, 。
。
又因为 ,所以
,所以 平面
平面 .
.
由 ,得
,得 平面
平面 . (14分)
. (14分)
17、解:(1)由题意知 ,
,
∴
由 ,可得
,可得

 (6分)
(6分)
(2)当 时,∵
时,∵
∴ ,两式相减得
,两式相减得
∴
 为常数,
为常数,
∴ ,
, ,
, ,…,
,…, 成等比数列。
成等比数列。
其中
 ,∴
,∴ ………(12分)
………(12分)
18、解:设二次函数 ,则
,则 ,解得
,解得
∴
将 代入上式:
代入上式:
而 对于,由已知,得:
对于,由已知,得: ,解得
,解得
∴
将 代入:
代入:
而4月份的实际产量为万件,相比之下,1.35比1.3更接近1.37.
∴选用函数作模型函数较好.
19、(1) ………(2分)
………(2分)
(1)由题意; ,解得
,解得 ,
,
∴所求的解析式为 ………(6分)
………(6分)
(2)由(1)可得
令 ,得
,得  或
或 , ………(8分)
, ………(8分)
∴当 时,
时,  ,当
,当 时,
时,  ,当
,当 时,
时, 
 因此,当
因此,当 时,
时,  有极大值
有极大值 ,………(8分)
,………(8分)
当 时,
时,  有极小值
有极小值 ,………(10分)
,………(10分)
∴函数 的图象大致如图。
的图象大致如图。
由图可知: 。………(14分)
。………(14分)
20、解:(1)直线 与
与 轴垂直时与抛物线交于一点,不满足题意.
轴垂直时与抛物线交于一点,不满足题意.
设直线 的方程为
的方程为 ,代入
,代入 得,
得,
 设
设 、
、 、
、
则 ,且
,且 ,即
,即 或
或 .
.
∴ ,
, 为
为 的中点.
的中点.
∴
∴ 由
由 或
或 得
得 或
或 .由
.由 在
在 轴右侧得.
轴右侧得. 
轨迹 的方程为
的方程为 .
.
(2)∵曲线 的方程为
的方程为 。
。
∴ ∴
∴  ,
,
 ,
, 且
且
∴ 又
又 ,
, ,
,
∴ ,
,
∴ ,∴
,∴
∴ 的取值范围为
的取值范围为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com