20080917
二、填空题
13.1 14.(-1,3) 15.5 16.②③④
三、解答题
17.解:(Ⅰ)
 ………………4分
………………4分

当 ……2分
……2分
(Ⅱ) ………3分
………3分
又
 ………………3分
………………3分
18.解:(Ⅰ)乙在第3次独立地射时(每次射击相互独立)才首次命中10环的概率为

(Ⅱ)甲、乙两名运动员各自独立射击1次,两人中恰有一人命中10环的概率为

19.解:(Ⅰ)以D为坐标原点,DA所在的直线为x轴、DC所在的直线为y轴、DP所在的直线为z轴,建立如图所示的空间直角坐标系D-xyz.
则A(1,0,0),B(1,1,0),C(0,1,0),
P(0,0,1)


(Ⅱ)


 、
、


解法二:
设平面BCE的法向量为
由
 ………………2分
………………2分
设平面FCE的法向量为
由

 …………2分
…………2分
20.(Ⅰ)由题意,得

(Ⅱ)①当

②当
令

21.解:(Ⅰ)设椭圆方程为
由题意,得
 所求椭圆方程
所求椭圆方程 ; ……………5分
; ……………5分
(Ⅱ)设抛物线C的方程为 .
.
由 .
.
 抛物线C的方程为
抛物线C的方程为

由
 ,设
,设 、
、 ,则有
,则有
 ,
, .
.

代入直线

22.解:(Ⅰ)


(Ⅱ)记方程①: 方程②:
方程②:
分别研究方程①和方程②的根的情况:
(1)方程①有且仅有一个实数根 方程①没有实数根
方程①没有实数根
(2)方程②有且仅有两个不相同的实数根,即方程 有两个不相同的非正实数根.
有两个不相同的非正实数根.

方程②有且仅有一个不相同的实数根,即方程 有且仅有一个蜚 正实数根.
有且仅有一个蜚 正实数根.

综上可知:当方程 有三个不相同的实数根时,
有三个不相同的实数根时,
当方程 有且仅有两个不相同的实数根时,
有且仅有两个不相同的实数根时,
 符合题意的实数
符合题意的实数 取值的集合为
取值的集合为


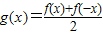 ,
,
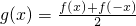 ,
,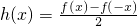
![]() 上满足
上满足![]() ,且在闭区间[0,7]上,只有
,且在闭区间[0,7]上,只有![]()
![]()
![]()
![]() 的奇偶性;
的奇偶性;![]() 在闭区间[-2005,2005]上的根的个数,并证明你的结论.
在闭区间[-2005,2005]上的根的个数,并证明你的结论.