练习册

  • 练习册
  • 试题
    (Ⅰ)证明:∥平面, 【查看更多】

     

    题目列表(包括答案和解析)

    平面内n条直线，其中任何两条不平行，任何三条不共点．
    （1）设这n条直线互相分割成f（n）条线段或射线，猜想f（n）的表达式并给出证明；
    （2）求证：这n条直线把平面分成
    n(n+1)2
    +1    个区域．

    查看答案和解析>>

    平面直角坐标系中，O为坐标原点，已知两点M（1，-3）、N（5，1），若点C满足
    OC
    =t
    OM
    +（1-t）
    ON
    （t∈R），点C的轨迹与抛物线：y2=4x交于A、B两点．
    （Ⅰ）求证：
    OA
    ⊥
    OB
    ；
    （Ⅱ）在x轴上是否存在一点P（m，0）（m∈R），使得过P点的直线交抛物线于D、E两点，并以该弦DE为直径的圆都过原点．若存在，请求出m的值及圆心的轨迹方程；若不存在，请说明理由．

    查看答案和解析>>

    平面ABDE⊥平面ABC，△ABC是等腰直角三角形，AC=BC=4，四边形ABDE是直角梯形，BD∥AE，BD⊥BA，BD=
    12
    AE=2    ，O、M分别为CE、AB的中点．
    （I）求证：OD∥平面ABC；
    （II）能否在EM上找一点N，使得ON⊥平面ABDE？若能，请指出点N的位置，并加以证明；若不能，请说明理由．

    查看答案和解析>>

    （）（本小题满分12分）

    如图，四棱锥S-ABCD 的底面是正方形，每条侧棱的长都是地面边长的倍，P为侧棱SD上的点。   

    （Ⅰ）求证：AC⊥SD；

    （Ⅱ）若SD⊥平面PAC，求二面角P-AC-D的大小

    （Ⅲ）在（Ⅱ）的条件下，侧棱SC上是否存在一点E，使得BE∥平面PAC。若存在，求SE：EC的值；若不存在，试说明理由。

    查看答案和解析>>

    （）选修4－1：几何证明讲

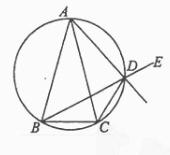    已知 ABC   中，AB=AC,  D是 ABC外接圆劣弧上的点（不与点A,C重合），延长BD至E。

    （1）       求证：AD的延长线平分CDE；

    （2）       若BAC=30，ABC中BC边上的高为2+，求ABC外接圆的面积。

    查看答案和解析>>

    一、选择题

    20080917

    二、填空题

    13．1　　　　14．（-1，3）　　　　15．5　　　　16．②③④

    三、解答题

    17．解：（Ⅰ）

    　　　　　　………………4分

    　　

    　　当　　　……2分

    （Ⅱ）　　………3分

    　　又

    　　　　　　　　　………………3分

    18．解：（Ⅰ）乙在第3次独立地射时（每次射击相互独立）才首次命中10环的概率为

    　　

    （Ⅱ）甲、乙两名运动员各自独立射击1次，两人中恰有一人命中10环的概率为

    　　

    19．解：（Ⅰ）以D为坐标原点，DA所在的直线为x轴、DC所在的直线为y轴、DP所在的直线为z轴，建立如图所示的空间直角坐标系D－xyz.

    　　则A（1，0，0），B（1，1，0），C（0，1，0），

    　　P（0，0，1）

    　　

    　　

       （Ⅱ）

    　　

    　　

    　　、

    　　

    　　

    　　解法二：

    　　设平面BCE的法向量为

    　　由

    　　　　　　　　　　　　　………………2分

    　　设平面FCE的法向量为

    　　由

    　　

    　　　　　　　…………2分

    20．（Ⅰ）由题意，得

    　　

       （Ⅱ）①当

    　　

    ②当

    　　令

    　　

    21．解：（Ⅰ）设椭圆方程为

    　　由题意，得

    所求椭圆方程；　　……………5分

    （Ⅱ）设抛物线C的方程为.

    　　由.

    　　抛物线C的方程为

    　　

    由，设、，则有

    ，.

    　　

    　　代入直线

    　　

    22．解：（Ⅰ）

    　　

    （Ⅱ）记方程①：方程②：

    　　分别研究方程①和方程②的根的情况：

       （1）方程①有且仅有一个实数根方程①没有实数根

       （2）方程②有且仅有两个不相同的实数根，即方程有两个不相同的非正实数根．

    　　

    　　方程②有且仅有一个不相同的实数根，即方程有且仅有一个蜚　正实数根．

    　　

    　　综上可知：当方程有三个不相同的实数根时，

    　　当方程有且仅有两个不相同的实数根时，

    　　符合题意的实数取值的集合为

     


    同步练习册答案