练习册

  • 练习册
  • 试题
    (Ⅱ)设数列的前n项和为求的最值． 【查看更多】

     

    题目列表(包括答案和解析)

     

        设数列的前n项和为，已知.

        （1）求数列的通项公式；

    （2）令 .用数学归纳法证明:

    ；

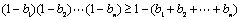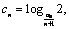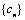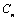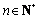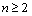    （3）设数列的前n项和为，若存在整数m,使对任意且，都有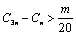成立，求m的最大值.

     

     

     

     

     

     

     

    查看答案和解析>>

    数列{}的前n项和为，，．

    （1）设，证明：数列是等比数列；

    （2）求数列的前项和；

    （3）若，．求不超过的最大整数的值。

     

    查看答案和解析>>

    数列{}的前n项和为，，．
    （1）设，证明：数列是等比数列；
    （2）求数列的前项和；
    （3）若，．求不超过的最大整数的值。

    查看答案和解析>>

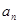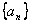    数列的前n项和为Sn=2n-1。
    （1）求；
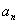    （2）设数列满足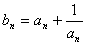，判断并证明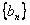的单调性；
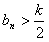    （3）对n∈N*，恒成立，求k的最大整数值。

    查看答案和解析>>

    数列{}的前n项和为，

    （Ⅰ）设，证明：数列｛｝是等比数列；

    （Ⅱ）求数列的前n项和；

    （Ⅲ）若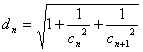，，，求不超过P的最大整数的值。

    查看答案和解析>>

    一、选择题

    20080917

    二、填空题

    13．1　　　　14．（-1，3）　　　　15．5　　　　16．②③④

    三、解答题

    17．解：（Ⅰ）

    　　　　　　………………4分

    　　

    　　当　　　……2分

    （Ⅱ）　　………3分

    　　又

    　　　　　　　　　………………3分

    18．解：（Ⅰ）乙在第3次独立地射时（每次射击相互独立）才首次命中10环的概率为

    　　

    （Ⅱ）甲、乙两名运动员各自独立射击1次，两人中恰有一人命中10环的概率为

    　　

    19．解：（Ⅰ）以D为坐标原点，DA所在的直线为x轴、DC所在的直线为y轴、DP所在的直线为z轴，建立如图所示的空间直角坐标系D－xyz.

    　　则A（1，0，0），B（1，1，0），C（0，1，0），

    　　P（0，0，1）

    　　

    　　

       （Ⅱ）

    　　

    　　

    　　、

    　　

    　　

    　　解法二：

    　　设平面BCE的法向量为

    　　由

    　　　　　　　　　　　　　………………2分

    　　设平面FCE的法向量为

    　　由

    　　

    　　　　　　　…………2分

    20．（Ⅰ）由题意，得

    　　

       （Ⅱ）①当

    　　

    ②当

    　　令

    　　

    21．解：（Ⅰ）设椭圆方程为

    　　由题意，得

    所求椭圆方程；　　……………5分

    （Ⅱ）设抛物线C的方程为.

    　　由.

    　　抛物线C的方程为

    　　

    由，设、，则有

    ，.

    　　

    　　代入直线

    　　

    22．解：（Ⅰ）

    　　

    （Ⅱ）记方程①：方程②：

    　　分别研究方程①和方程②的根的情况：

       （1）方程①有且仅有一个实数根方程①没有实数根

       （2）方程②有且仅有两个不相同的实数根，即方程有两个不相同的非正实数根．

    　　

    　　方程②有且仅有一个不相同的实数根，即方程有且仅有一个蜚　正实数根．

    　　

    　　综上可知：当方程有三个不相同的实数根时，

    　　当方程有且仅有两个不相同的实数根时，

    　　符合题意的实数取值的集合为

     


    同步练习册答案