练习册

  • 练习册
  • 试题
    15． 【查看更多】

     

    题目列表(包括答案和解析)

    （本题满分13分）

    已知数列满足，

    （1）计算的值；

    （2）由（1）的结果猜想的通项公式，并证明你的结论。

    查看答案和解析>>

    （本题满分13分）

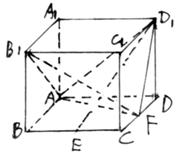
    如图在棱长为2的正方体中，点F为棱CD中点，点E在棱BC上

    （1）确定点E位置使面；

    （2）当面时，求二面角的平面角的余弦值；

     

     

     

     

     

     

     

     

     

    查看答案和解析>>

    （本题满分13分）

    一个口袋里有4个不同的红球，6个不同的白球（球的大小均一样）

    （1）从中任取3个球，恰好为同色球的不同取法有多少种？

    （2）取得一个红球记为2分，一个白球记为1分。从口袋中取出五个球，使总分不小于7分的不同取法共有多少种？

    查看答案和解析>>

    （本题满分13分）已知定义域为[0,1]的函数同时满足：  ①对于任意的,总有;  ②=1;     ③当时有.

    (1)求的值；w.w.w.k.s.5.u.c.o.m        

    (2)求的最大值；

    (3)当对于任意，总有成立，求实数的取值范围.

    查看答案和解析>>

    （本题满分13分）

    已知椭圆的左、右焦点分别为、，过的直线交椭圆于、两点，过的直线交椭圆于、两点，且，垂足为．

    （1）设点的坐标为，求的最值；

    （2）求四边形的面积的最小值．

    查看答案和解析>>

    一、选择题（本大题共有8个小题，每小题5分，共40分；在每个小题给出的四个选项中有且仅有一个符合题目要求的）

    题号

    1

    2

    3

    4

    5

    6

    7

    8

    答案

    B

    D

    C

    C

    B

    A

    C

    B

    二、填空题（本大题共有6个小题，每小题5分，共30分；请把答案填在相应的位置）

    题号

    9

    10

    11

    12

    13

    14

    答案

    -1+

    8,70

    24

    ①③④

    三、解答题（本大题共6个小题，共80分；解答应写出文字说明，证明过程或演算步骤）

    15．（本题满分13分）

        解：（1）

               

               

           （2）由题意，得

               

    16．（本题满分13分）

        解：（1）这3封信分别被投进3个信箱的概率为

               

           （2）恰有2个信箱没有信的概率为

               

           （3）设信箱中的信箱数为

                        

                        

    0

    1

    2

    3

    17．（本题满分13分）

        解：解答一：（1）在菱形中，连接则是等边三角形。

                      

    （2）

                      

                      

                  （3）取中点，连结

                      

         解法二：（1）同解法一；

                （2）过点作平行线交于,以点为坐标原点,建立如图的坐标系

                      

                       二面角的大小为

                  （3）由已知，可得点

                      

                       即异面直线所成角的余弦值为

    18．（本题满分13分）

    解：（1）将函数的图象向右平移一个单位，得到函数的图象，

            函数的图象关于点（0，0）对称，即函数是奇函数，

           

           

            由题意得：

            所以

       （2）由（1）可得

            故设所求两点为

           

            满足条件的两点的坐标为：

    （3）

           

           

    19．（本题满分14分）

    解：（1）椭圆的右焦点的坐标为（1，0），

           

    （2）

          

      （3）由（2）知

          

    20．（本题满分14分）

    解：（1）

               

           （2）由（1）知

               

           （3）

               

     

     


    同步练习册答案