一、选择题:本大题共12个小题,每小题5分,共60分。
1―5 BCBAB 6―10 DCCCD 11―12 DB
二、填空题:本大题共4个小题,每小题4分,共16分。
13. 14.1:2 15.①②⑤ 16.⑤
14.1:2 15.①②⑤ 16.⑤
20090203 17.(本小题满分12分) 解:(I) 共线 共线   ………………3分 ………………3分 故 …………6分 …………6分 (II)   …………12分 …………12分 18.(本小题满分12分) 解:根据题意得图02,其中BC=31千米,BD=20千米,CD=21千米, ∠CAB=60˚.设∠ACD = α ,∠CDB = β .

 , ,
 . .


 .……9分 .……9分
在△ACD中,由正弦定理得:  . .

19.(本小题满分12分) 解:(1)连结OP,∵Q为切点,PQ OQ, OQ, 由勾股定理有, 又由已知 即: 化简得 …………3分 …………3分 (2)由 ,得 ,得  …………6分 …………6分
故当 时, 时, 线段PQ长取最小值 线段PQ长取最小值 …………7分 …………7分 (3)设⊙P的半径为R,∵⊙P与⊙O有公共点,⊙O的半径为1, ∴ 即R 即R 且R 且R 而 故当 时, 时, ,此时b=―2a+3= ,此时b=―2a+3= 得半径最最小值时⊙P的方程为 …………12分 …………12分 20.(本小题满分12分) 解:(I)过G作GM//CD交CC1于M,交D1C于O。

∵G为DD1的中点,∴O为D1C的中点 从而GO 故四边形GFBO为平行四边形…………3分 ∴GF//BO 又GF 平面BCD1,BO 平面BCD1,BO 平面BCD1 平面BCD1 ∴GF//平面BCD1。 …………5分 (II)过A作AH⊥DE于H, 过H作HN⊥EC于N,连结AN。 ∵DC⊥平面ADD1A1,∴CD⊥AH。 又∵AH⊥DE,∴AH⊥平面ECD。 ∴AH⊥EC。 …………7分 又HN⊥EC ∴EC⊥平面AHN。 故AN⊥∴∠ANH为二面角A―CE―D的平面角 …………9分 在Rt△EAD中,∵AD=AE=1,∴AH= 在Rt△EAC中,∵EA=1,AC= ∴ …………12分 …………12分 21.(本小题满分12分) 解:(I) 
(II) 
(III)令 上是增函数 上是增函数 

22.(本小题满分12分) 解:(I)  单调递增。 …………2分 单调递增。 …………2分
① ,不等式无解; ,不等式无解; ② ; ; ③ ; ; 所以 …………5分 …………5分
(II) , …………6分 , …………6分 
…………8分 因为对一切 ……10分 ……10分
(III)问题等价于证明 , , 由(1)可知
…………12分 设 易得 当且仅当 成立。 成立。
…………14分
| | | | | | | |

 (
( 且
且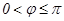 )为奇函数,其图象与
)为奇函数,其图象与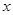 轴的所有交点中最近的两交点间的距离为
轴的所有交点中最近的两交点间的距离为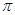 ,则
,则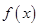 的一个单调递增区间为 ( )
的一个单调递增区间为 ( ) B.
B. C.
C.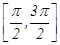 D.
D.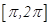
 14.1:2 15.①②⑤ 16.⑤
14.1:2 15.①②⑤ 16.⑤