
题目列表(包括答案和解析)
| a+m |
| b+m |
| a |
| b |
给出下列命题,其中正确命题的个数为( )
①在区间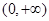 上,函数
上,函数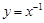 ,
,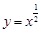 ,
,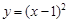 ,
,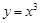 中有三个是增函数;
中有三个是增函数;
②命题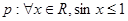 .则
.则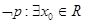 ,使
,使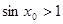 ;
;
③若函数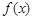 是偶函数,则
是偶函数,则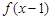 的图象关于直线
的图象关于直线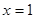 对称;
对称;
④已知函数 则方程
则方程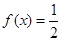 有
有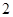 个实数根.
个实数根.
A.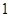 B.
B.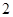 C.
C.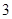 D.
D.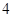
给出下列命题,其中正确命题的个数为( )
①在区间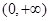 上,函数
上,函数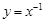 ,
,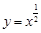 ,
,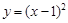 ,
,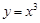 中有三个是增函数;
中有三个是增函数;
②命题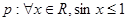 .则
.则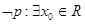 ,使
,使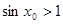 ;
;
③若函数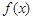 是偶函数,则
是偶函数,则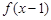 的图象关于直线
的图象关于直线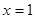 对称;
对称;
④已知函数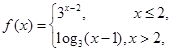 则方程
则方程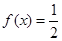 有
有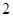 个实数根.
个实数根.
A.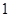 | B.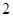 | C.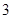 | D.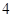 |
一、选择题:本大题共12小题,每小题5分,共60分。
ABBD DBBA BCBA
二、填空题:本大题共4小题,每小题4分,共16分。
13.2 14.3 15. 16.①③
16.①③
三、解答题:本大题共6小题,共74分。解答应写出文字说明、证明过程或演算步骤。
17.解:(I) ………2分
………2分
依题意函数
所以 …………4分
…………4分

(II)

18.解:(I)由题意得:上年度的利润的 万元;
万元;
本年度每辆车的投入成本为 万元;
万元;
本年度每辆车的出厂价为 万元;
万元;
本年度年销售量为 ………………2分
………………2分
因此本年度的利润为

(II)本年度的利润为

………………7分
则
由 (舍去)。 …………9分
(舍去)。 …………9分
|