练习册

  • 练习册
  • 试题
    (本小题满分14分) 【查看更多】

     

    题目列表(包括答案和解析)

    （本小题满分１2分）

    　已知ABC的三个顶点的直角坐标分别为A(3,4)、B(0,0)、Ｃ(c,0)

    若c=5，求sin∠A的值；

    若∠A为钝角，求c的取值范围；

    查看答案和解析>>

    （本小题满分１３分）

      袋中有五张卡片，其中红色卡片三张，标号分别为1，2，3；蓝色卡片两张，标号分

       为1，2.

     (Ⅰ)从以上五张卡片中任取两张，求这两张卡片颜色不同且标号之和小于4的概率；

     (Ⅱ)现袋中再放入一张标号为0的绿色卡片，从这六张卡片中任取两张，求这两张卡

         片颜色不同且标号之和小于4的概率.

     

    查看答案和解析>>

    （本小题满分１２分）

    某服装商场为了了解毛衣的月销售量y(件)与月平均气温x(℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表：

    (1) 算出线性回归方程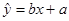; (a,b精确到十分位)

    (2)气象部门预测下个月的平均气温约为6℃,据此估计,求该商场下个月毛衣的销售量.

     

    查看答案和解析>>

    （本小题满分１２分）某企业员工500人参加“学雷锋”志愿活动，按年龄分组：第1组[25，30)，第2组[30，35)，第3组[35，40)，第4组[40，45)，第5组[45，50]，得到的频率分布直方图如右图所示．

    (1)下表是年龄的频数分布表，求正整数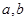的值；

    区间

    [25，30)

    [30，35)

    [35，40)

    [40，45)

    [45，50]

    人数

    50

    50

    150

     

     

     

     

     

    (2)现在要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人，年龄在第1,2,3组的人数分别是多少？

    (3)在(2)的前提下，从这6人中随机抽取2人参加社区宣传交流活动，求至少有1人年龄在第3组的概率．

     

    查看答案和解析>>

    （本小题满分１2分）

    　已知ABC的三个顶点的直角坐标分别为A(3,4)、B(0,0)、Ｃ(c,0)

    （１）  若c=5，求sin∠A的值；

    （２）  若∠A为钝角，求c的取值范围；

     

    查看答案和解析>>

    1―5、  CDDCA   6―10、DABAB    11、    12、1,  9

    13解：因为方程x 2 + mx + 1=0有两个不相等的实根，

    所以Δ1=m 2 ? 4>0,  ∴m>2或m < ? 2               

    又因为不等式4x 2 +4(m ? 2)x + 1>0的解集为R，

    所以Δ2=16(m ? 2) 2? 16<0,   ∴1< m <3            

    因为p或q为真，p且q为假，所以p与q为一真一假， 

    （1）当p为真q为假时，

    （2）当p为假q为真时，    

    综上所述得：m的取值范围是或

    14、解:  直线方程为y=-x+4,联立方程,消去y得,.

    设A(),B(),得

    所以:,

    由已知可得+=0,从而16-8p=0,得p=2.

    所以抛物线方程为y2=4x,焦点坐标为F(1,0)

    15、解（Ⅰ） AC与PB所成角的余弦值为.

     （Ⅱ）N点到AB、AP的距离分别为1，.

    16解:   （1）； （2）略

    17、6        18、①②③⑤         19、B     20、B

    21、解：（1）略  （2）

    22、解：（1）设双曲线C的渐近线方程为y=kx，则kx-y=0

    ∵该直线与圆 相切，∴双曲线C的两条渐近线方程为y=±x．

    故设双曲线C的方程为．又双曲线C的一个焦点为，

    ∴，∴双曲线C的方程为:.

    （2）由得．令

    ∵直线与双曲线左支交于两点，等价于方程f(x)=0在上有两个

    不等负实根．

    因此，解得．．                       

    （3）. ∵ AB中点为，

    ∴直线l的方程为：． 令x=0，得．

    ∵，∴，∴．     

     

     

     

     

     

     


    同步练习册答案