
题目列表(包括答案和解析)
在△ABC中,顶点A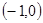 ,B
,B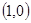 ,动点D,E满足:①
,动点D,E满足:①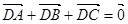 ;②
;②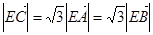 ,③
,③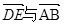 共线.
共线.
(Ⅰ)求△ABC顶点C的轨迹方程;
(Ⅱ)若斜率为1直线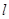 与动点C的轨迹交与M,N两点,且
与动点C的轨迹交与M,N两点,且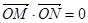 ,求直线
,求直线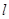 的方程.
的方程.
在△ABC中,顶点A(-1,0),B(1,0),动点D,E满足:①![]() ;②
;②![]() ,③
,③![]() 共线.
共线.
(Ⅰ)求△ABC顶点C的轨迹方程;
(Ⅱ)若斜率为1直线l与动点C的轨迹交与M,N两点,且![]() ,求直线l的方程.
,求直线l的方程.
在△ABC中,顶点A(-1,0),B(1,0),动点D,E满足:①![]() ;②
;②![]() ,③
,③![]() 共线.
共线.
(Ⅰ)求△ABC顶点C的轨迹方程;
(Ⅱ)是否存在圆心在原点的圆,只要该圆的切线与顶点C的轨迹有两个不同交点M,N,就一定有![]() ,若存在,求该圆的方程;若不存在,请说明理由.
,若存在,求该圆的方程;若不存在,请说明理由.
在△
ABC中,顶点A(-1,0),B(1,0),动点D,E满足:①![]() +
+![]() +
+![]() =
=![]() ;
;
②|![]() |=
|=![]() |
|![]() |=
|=![]() |
|![]() |
|
③![]() 与
与![]() 共线.
共线.
(Ⅰ)求△ABC顶点C的轨迹方程;
(Ⅱ)若斜率为1直线l与动点C的轨迹交于M,N两点,且![]() ·
·![]() =0,求直线l的方程.
=0,求直线l的方程.
| ||
| 7 |
| ||
| 7 |
| MA |
| MB |
| MC |
| 0 |
| NC |
| 7 |
| NA |
| 7 |
| NB |
| MN |
| AB |
| PE |
| PF |
一、选择题(每小题5分,共40分)
1.D 2.B 3.B 4.B 5.C 6.D 7.C 8.A
解:5.C
 ,相切时的斜率为
,相切时的斜率为
6.D

7.C 

8.A 原方程可化为[(3x+y)2009+(3x+y)]+(x2009+x)=0,设函数f(x)=x2009+x,
显然该函数为奇函数,且在R上是增函数,则原方程为f(3x+y)+f(x)=0,
即f(3x+y)=-f(x)= f(-x),所以3x+y=-x,故4x+y=0
二、填空题(每小题5分,共30分)
9. 
10.
 位执“一般”对应
位执“一般”对应 位“不喜欢”,即“一般”是“不喜欢”的
位“不喜欢”,即“一般”是“不喜欢”的 倍,而他们的差为
倍,而他们的差为 人,即“一般”有
人,即“一般”有 人,“不喜欢”的有
人,“不喜欢”的有 人,且“喜欢”是“不喜欢”的5倍,即
人,且“喜欢”是“不喜欢”的5倍,即 人.
人.
11.-192
12. ;根据题中的信息,可以把左边的式子归纳为从
;根据题中的信息,可以把左边的式子归纳为从 个球(n个白球,k个黑球中取出m个球,可分为:没有黑球,一个黑球,……,k个黑球等
个球(n个白球,k个黑球中取出m个球,可分为:没有黑球,一个黑球,……,k个黑球等 类,故有
类,故有 种取法.
种取法.
13.5; 14、 ;
;
15.16; 由 可化为xy =8+x+y,
可化为xy =8+x+y,  x,y均为正实数
x,y均为正实数
 xy
=8+x+y
xy
=8+x+y
(当且仅当x=y等号成立)即xy-2 -8
-8 可解得
可解得
 ,
,
即xy 16故xy的最小值为16.
16故xy的最小值为16.
三、解答题:(本大题共6小题,共80分,解答应写出文字说明,证明过程或演算步骤)。
16、(本题满分12分)
解:Ⅰ)在 中,
中, 且
且 
cosA= ,又A是
,又A是 的内角,∴A=
的内角,∴A= …………6分
…………6分
(Ⅱ)由正弦定理,又 ,故
,故 …………8分
…………8分
即: 故
故 是以
是以 为直角的直角三角形 …………10分
为直角的直角三角形 …………10分
又∵A= , ∴B=
, ∴B= …………12分
…………12分
17.(本题满分14分)
解:(I)所求x的可能取值为6、7、8、9 …………1分


…………7分
(II)
∴线路通过信息量的数学期望
EX ……13分
……13分
答:(I)线路信息畅通的概率是 . (II)线路通过信息量的数学期望是
. (II)线路通过信息量的数学期望是 .……14分
.……14分
18.(本题满分14分)
解:(Ⅰ)建立如图所示的空间直角坐标系, ……1分
|