题目列表(包括答案和解析)
（本小题满分12分）
已知双曲线
的离心率为2，焦点到渐近线的距离等于
，过右焦点
的直线
交双曲线于
、
两点，
为左焦点，
（Ⅰ）求双曲线的方程；
（Ⅱ）若
的面积等于
，求直线
的方程．
（本小题满分12分）已知双曲线
的两个焦点为
、
点
在双曲线C上.
(1)求双曲线C的方程；
(2)记O为坐标原点，过点Q (0,2)的直线l与双曲线C相交于不同的两点E、F，若△OEF的面积为
求直线l的方程.
（本小题满分12分）已知双曲线的一条渐近线方程是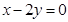
，若双曲线经过点
，求此双曲线的标准方程。
（本小题满分12分）
已知双曲线
的离心率为
，且过点P（
）.
(1)求双曲线C的方程；
(2)若直线
与双曲线C恒有两个不同的交点A,B,且
（其中O为原点），求k的取值范围.
（本小题满分12分）
已知双曲线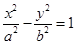
的离心率为2，焦点到渐近线的距离等于
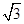，过右焦点
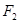的直线
交双曲线于
、
两点，
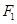为左焦点．
（Ⅰ）求双曲线的方程；
（Ⅱ）若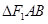
的面积等于
，求直线
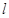的方程．
一、选择题（本大题共12小题，每小题4分，共48分）
1.C 2.A 3.D 4.D 5.D 6.B 7.C 8.D 9.C 10.A
二、填空题（本大题共4小题，每小题4分，共16分）
13.
x∈R，x≤0
14.－15 15.－1 16.
三、解答题（本大题共3小题，每小题12分，共36分）
17.(本小题满分12分)
解：（Ⅰ）由已知c＝1，则a2－b2＝1．
又
故a2＝4，b2＝3.
所求椭圆方程为
．……………………………………………6分
（Ⅱ）由
解得
又
，
于是
……………………………………12分
18.（本小题满分12分）
解：（Ⅰ）因为双曲线的焦点在y轴上，设所求双曲线的方程为
．
由题意，得
解得a＝2，b＝1．
所求双曲线的方程为
…………………………………………6分
（Ⅱ）由（Ⅰ）可求得F1（0，－
），F2（0，）．
点F1，F2关于直线y＝x的对称点分别为F1′（－，0），F2′（，0），又P（0，2），设椭圆方程为
（m＞n＞0）．
由椭圆定义，得
因为m2－n2＝5，所以n2＝4．
所以椭圆的方程为
.………………………………………12分
19.（本小题满分12分）
证明：如图，建立空间直角坐标系A－xyz，设AB＝
则A（0，0，0），B（
∵E为AB的中点，F为PC的中点，
∴E（a，0，0），F（a，b，c）.
（Ⅰ）∵
＝（0，b，c），
＝（0，0，
＝（0，2b，0），
∴＝
（＋）.
∴与、共面.
又∴
平面PAD，
∴EF∥平面PAD.……………………4分
（Ⅱ）∵
=（
∴?＝（
∴EF
CD.…………………………………………………………8分
（Ⅲ）若∠PDA＝45°则有2b＝
∴＝（0，b，b），＝（0，0，2b）.
∴
＜，＞＝
∴＜，＞＝45°.
∵AP平面ABCD，
∴是平面ABCD的法向量.
∴EF与平面ABCD所成的角为90°－＜，＞＝45°.……12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com