
题目列表(包括答案和解析)
集合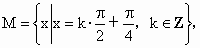
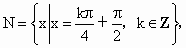 则
则
[ ]
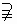 N
N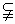 N
N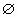
集合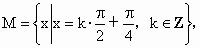
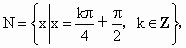 则
则
[ ]
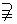 N
N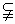 N
N
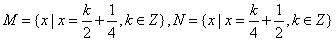 ,则
,则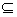 N
N 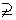 N
N 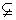 N
N
A.(几何证明选讲选做题)
如图,已知AB为圆O的直径,BC切圆O于点B,AC交圆O于点P,E为线段BC的中点.求证:OP⊥PE.

B.(矩阵与变换选做题)
已知M= ,N=
,N= ,设曲线y=sinx在矩阵MN对应的变换作用下得到曲线F,求F的方程.
,设曲线y=sinx在矩阵MN对应的变换作用下得到曲线F,求F的方程.
C.(坐标系与参数方程选做题)
在平面直角坐标系xOy中,直线m的参数方程为 (t为参数);在以O为极点、射线Ox为极轴的极坐标系中,曲线C的极坐标方程为ρsinθ=8cosθ.若直线m与曲线C交于A、B两点,求线段AB的长.
(t为参数);在以O为极点、射线Ox为极轴的极坐标系中,曲线C的极坐标方程为ρsinθ=8cosθ.若直线m与曲线C交于A、B两点,求线段AB的长.
D.(不等式选做题)
设x,y均为正数,且x>y,求证:2x+ ≥2y+3.
≥2y+3.
设集合M = ,N =
,N = ,则 ( )
,则 ( )
A.M=N B.M N C.M
N C.M N D.M
N D.M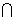 N=
N=
一、选择题:
1.C 2.D 3.D 4.C 5. B 6.C 7. C 8.C 9. A
|