练习册

  • 练习册
  • 试题
    (1)当a.b间的电压为U1时.在M.N间加上适当的电压U2.使离子到达探测器.请导出离子的全部飞行时间与比荷K的关系式.(2)去掉偏转电压U2.在M.N间区域加上垂直于纸面的匀强磁场.磁感应强度B.若进入a.b间所有离子质量均为m.要使所有的离子均能通过控制区从右侧飞出.a.b间的加速电压U1至少为多少? 【查看更多】

     

    题目列表(包括答案和解析)

    飞行时间质谱仪主要由脉冲阀、激光器、加速电场、偏转电场和探测器组成，可以对气体分子进行分析。如图所示，脉冲阀P喷出微量气体，经激光照射产生不同价位的离子，自a板小孔进入a、b间的加速电场，从b板小孔射出，沿中线方向进入M、N板间的偏转控制区，到达探测器。已知加速电场a、b板间距为d，偏转电场极板M、N的长度为L1，宽度为L2。不计离子重力及进入a板时的初速度。
    （1）设离子带电粒子比荷为k（k=q/m），如a、b间的加速电压为U1，试求离子进入偏转电场时的初速度v0；
    （2）当a、b间的电压为U1时，在M、N间加上适当的电压U2，离子从脉冲阀P喷出到到达探测器的全部飞行时间为t。请推导出离子k比荷的表达式；
    （3）在某次测量中探测器始终无法观察到离子，分析原因是离子偏转量过大，打到极板上，请说明如何调节才能观察到离子？

    查看答案和解析>>

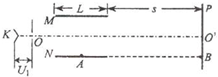    精英家教网真空室中有如图所示的装置，设电子电量为e、质量为m．电极K发出的电子（初速不计）经过加速电场后，由小孔O沿水平放置的偏转板M、N间的中心轴线OO'射入．M、N板长为L，两板间的距离d，两板间加有恒定电压U2，它们间的电场可看作匀强电场．偏转板右端边缘到荧光屏P的距离为s．当加速电压为U1时，电子恰好打在荧光屏的B点．已知A、B点到中心轴线OO′的距离相等．求U1．

    查看答案和解析>>

    飞行时间质谱仪可对气体分子进行分析．如图所示，在真空状态下，脉冲阀P喷出微量气体，经激光照射产生电荷量为q、质量为m的正离子，自a板小孔进入a、b间的加速电场（a、b间的电压为U1），从b板小孔射出，沿中线方向进入M、N板间的偏转控制区，到达探测器．已知a、b板间距为d，极板M、N的长度和间距均为L．不计离子重力及进入a板时的初速度．则：
    （1）在M、N间加上适当的电压，使离子到达探测器．求离子到达探测器的全部飞行时间．
    （2）为保证离子不打在极板上，求M、N间的最大偏转电压U2．
    （3）求离子离开偏转控制区时的最大速率．

    查看答案和解析>>

    飞行时间质谱仪可对气体分子进行分析．如图所示，在真空状态下，脉冲阀P喷出微量气体，经激光照射产生电荷量为q、质量为m的正离子，自a板小孔进入a、b间的加速电场，从b板小孔射出，沿中线方向进入M、N板间的偏转控制区，到达探测器．已知a、b板间距为d，极板M、N的长度和间距均为L．不计离子重力及进入a板时的初速度．（1）当a、b间的电压为U1，在M、N间加上适当的电压U2，使离子到达探测器．求离子到达探测器的全部飞行时间．
    （2）为保证离子不打在极板上，试求U2与U1的关系．

    查看答案和解析>>

    飞行时间质谱仪可对气体分子进行分析。如图所示，在真空状态下，脉冲阀P喷出微量气体，经激光照射产生电荷量为q、质量为m的正离子，自a板小孔进入a、b间的加速电场，从b板小孔射出，沿中线方向进入M、N板间的偏转控制区，到达探测器。已知a、b板间距为d，极板M、N的长度和间距均为L。不计离子重力及进入a板时的初速度。

       （1）当a、b间的电压为U1，在M、N间加上适当的电压U2，使离子到达探测器。求离子从a板到达探测器的飞行时间。

       （2）为保证离子不打在极板上，试求U2与U1的关系。

    查看答案和解析>>

    一

    题号

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    11

    12

    答案

    B

    BD

    CD

    A

    A

    AD

    AB

    A

    C

    CD

    A

    ACD

    二

    13（1）D （5分）   (2)   80J （5分）   14 (1) A （5分） (2) ×10 8 m/s （5分）     

    15．（12分）4.0（3分）， 2.16 或2.2（3分），滑块的质量（3分），（3分）

    16 （12分）

    (1)  连接电路如答案图（5分）          (2) A （2分） (3) 1.6×103℃ （5分）

     

     

     

     

     

     

     

     

     

     

     

    17（18分）（1）．解：①设该星球表面的重力加速度为g小球的上升时间为，

    20081125

    解得      （2分）

       ②在该星球表面上小球所受万有引力为

         （2分）

    （1分）.

    (2) ①从B到C的过程中，加速度大小为a1＝＝2 m/s2  （2分），

    又a1＝mg，所以m＝0.2                            （2分），

    ②从A到B的过程中，加速度大小为a2    

    根据牛顿第二定律 mgsinq－mmgcosq＝ma2    （2分），

    a2＝4.4 m/s2

                       a2＝＝4.4 m/s2             （2分），

                         VA=2.0 m/s                  （1分）

    18（16分）

    解：设导体杆切割磁感线产生的感应电动势为E，感应电流为I。外电路为ad、dc、cb三边电阻串联后再与ab边电阻并联，设总电阻为R，ab边和dc边的电流分别为Iab和Idc。

    ⑴ 金属框受重力和安培力，处于静止状态，有：

                    (3分)

         (2分)

    =7.5A             (3分)

     

    ⑵    E＝B1L1                     (3分)

    E＝IR ， ，           (2分)

    得：          (3分)

           

    19题（17分）

    （1）由动能定理：                          ( 2分）

    n价正离子在a、b间的加速度                   ( 1分)

    在a、b间运动的时间=d                     ( 2分)

    在MN间运动的时间：t2=L/v                               ( 1分)

    离子到达探测器的时间：

    t=t1+t2=                                              ( 2分)

    （2）假定n价正离子在磁场中向N板偏转，洛仑兹力充当向心力，设轨迹半径为R，由牛顿第二定律得：                                 (   2分)

    离子刚好从N板右侧边缘穿出时，由几何关系：            

    R2=L2+（R-L/2）2                                         (2分)

    由以上各式得：                           ( 2分)

    当n=1时U1取最小值                     ( 3分)

    20．（17分）

    （1）设A在C板上滑动时，B相对于C板不动，据题意对B、C分析有：

    μmg=2ma，得，                       ( 1分)

    又B最大的加速度为由于am>a，所以B相对于C不滑动而一起向右做匀加速运动，则。                       ( 2分)

    （2）若物块A刚好与物块B发生碰撞，则A相对于C运动到B所在处时，A、B的速度大小相等，因为B与木板C的速度相等，所以此时三者的速度均相同，设为v1，由动量守恒定律得：

    mv0=3mv1        ①                 ( 2分)

     

    在此过程中，设木板C运动的路程为s1，则A运动的路程为s1+L，如图所示，由动能定理得

     

     

    对B、C系统有  ②           ( 2分)

    对A有    ③       (2分)

    联立①、②、③解得：，欲使A与B发生碰撞，须满足

                                       ( 2分)

       

    设B刚好不滑离木板C，此时三者的共同速度为v2，同理得

    mv0=3mv2          ④      (2分)

    在此过程中，A、B、C系统克服滑动摩擦力做功，减少的机械能转化为系统的内能，由能的转化和守恒得       ⑤   ( 2分)

    联立④、⑤解得

    综上所述，使物块A能与B发生碰撞，而B又不滑离C，则物块A的初速度v0应满足

    。                         (2分)

     

     

     

     

     

     

     

     

     

     


    同步练习册答案