
题目列表(包括答案和解析)
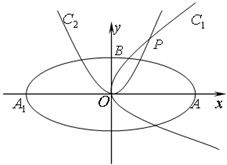 如图,椭圆C:
如图,椭圆C:| x2 |
| a2 |
| y2 |
| 2 |
| 2 |
| 2 |
| QM |
| QN |
 如图,椭圆C:
如图,椭圆C:| x2 |
| a2 |
| y2 |
| a2-1 |
| AP |
| BP |
如图,椭圆C: 的焦点在x轴上,左、右顶点分别为A1、A,上顶点为B.抛物线C1、C2分别以A、B为焦点,其顶点均为坐标原点O,C1与C2相交于直线
的焦点在x轴上,左、右顶点分别为A1、A,上顶点为B.抛物线C1、C2分别以A、B为焦点,其顶点均为坐标原点O,C1与C2相交于直线 上一点P.
上一点P.
(1)求椭圆C及抛物线C1、C2的方程;
(2)若动直线l与直线OP垂直,且与椭圆C交于不同两点M、N,已知点 ,求
,求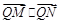 的最小值.
的最小值.

如图,椭圆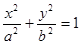
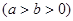 的左、右顶点分别是
的左、右顶点分别是 ,
, ,左、右焦点分别是
,左、右焦点分别是 ,
,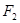 ,若
,若 ,
,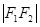 ,
, 成等比数列,则此椭圆的离心率为
成等比数列,则此椭圆的离心率为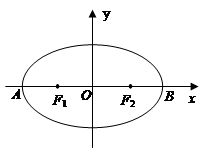
A.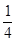 | B.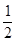 | C.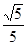 | D. |
1.D 2.B 3.C 4.B 5.A 6.B 7.B 8.D 9.C 10.C
l1.A 12.C
13.
14.15
15.
16.
提示:
1.D  .
.
2.B 视力住0.9以上的频率为 ,人数为
,人数为 .
.
3.C  ,且
,且
若 ,则
,则 且
且
反之,若 ,则
,则
4.B  ,由
,由 ,得
,得 .
.
 .
.
5.A  .
.
6.B 
当 时,
时, ,由
,由 得
得 ;
;
当 时,
时, ;
;
当 时,
时, ,由
,由 .
.
7.B 该几何体是上面是正四棱锥,下面为正方体,体积为
 .
.
8.D  .
.
9.C  ,
,
 ,
,
 ,
,
 ,
,
 .
.
10.C 
即 ,或
,或 .
.
 设
设 .
.
则 方程为
方程为 .
.
 过点
过点

 ,
,
 ,
,
 ,
,
 .
.
12.C
画出平面区域 ,
,
圆 的圆心
的圆心 ,半径为l,
,半径为l,
 的最大值为
的最大值为 的最小值为
的最小值为
 .
. 的最大值为
的最大值为 ,最小值为
,最小值为
13. .
.
 ,
,  .
.
14.15  ;
;
 ;
;
 .
.
15.






 .
.
16. .
.
又


17.解:(1) , (2分)
, (2分)
 . (4分)
. (4分)
由余弦定理,得 . (6分)
. (6分)
(2) , (7分)
, (7分)
 (9分)
(9分)  (10分)
(10分)
 (11分)
(11分)
 (12分)
(12分)
18.解:(1) 的可能取值为l,2,3,4.
的可能取值为l,2,3,4.

 (4分)
(4分)
∴甲取球次数 的数学期望
的数学期望 . (6分)
. (6分)
(2)由题意,两人各自从自己的箱子里任取一球比颜色
共有 (种)不同情形,
(8分)
(种)不同情形,
(8分)
每种情形都是等可能,记甲获胜为事件A,则
 (11分)
(11分)
所以甲获胜的概率小于乙获胜的概率,这个游戏规则不公平 (12分)
 19.解:以
19.解:以 为原点,
为原点, 、
、 、
、 所在的直线为
所在的直线为
 ,
, ,
, 轴,建立如图所示的空间直角坐标系,
轴,建立如图所示的空间直角坐标系,
则


 (3分)
(3分)
(1) ,
,

即直线 与
与 所成角的余角的余弦值为
所成角的余角的余弦值为 (6分)
(6分)
(2)设
由 平面
平面 得
得
即 得
得
 ,即
,即 为
为 的中点. (9分)
的中点. (9分)
(3)由(2)知 为平面
为平面 的法向量.
的法向量.
设 为平面
为平面 的法向量,
的法向量,

由 即
即
令 得
得 ,
,
 ,
,
即二面角 的余弦值为
的余弦值为
 (12分)
(12分)
(非向量解法参照给分)
20.(1)解: 成等比数列,
成等比数列, ,即
,即
又 , (3分)
, (3分)
 (5分)
(5分)
(2)证明:  . (6分)
. (6分)
 是首项为2,公差为2的等差数列,
是首项为2,公差为2的等差数列,
 (7分)
(7分)

 (当且仅当
(当且仅当 时取“=”). ① (9分)
时取“=”). ① (9分)

当且仅当 即
即 时取“=”. ② (11分)
时取“=”. ② (11分)
又①②中等号不可能同时取到, (12分)
(12分)
21.解:(1)设 .
.
对称轴方程 .由题意
.由题意 恒成立, (2分)
恒成立, (2分)
 在区间
在区间 上单凋递增, (3分)
上单凋递增, (3分)
∴当且仅当椭圆 上的点
上的点 在椭圆的左、右顶点时
在椭圆的左、右顶点时 取得最小值与最大值.(4分)
取得最小值与最大值.(4分)
(安徽高中数学网站注:这里用椭圆第二定义根简单直观)
(2)由已知与(1)得: ,
,
 , (5分)
, (5分)
∴椭圆的标准方程为 . (6分)
. (6分)
(3)设 ,联立
,联立
得 . (7分)
. (7分)
则
又 ,(8分)
,(8分)
∵椭圆的右顶点为 ,
,



 (9分)
(9分)
解得: ,且均满足
,且均满足 , (10分)
, (10分)
当 时,
时, 的方程为
的方程为 ,直线过定点(2,0),与已知矛盾.
,直线过定点(2,0),与已知矛盾.
当 时,
时, 的方程为
的方程为 ,直线过定点(
,直线过定点( ,0), (11分)
,0), (11分)
∴直线 过定点,定点坐标为(
过定点,定点坐标为( ,0). (12分)
,0). (12分)
22,解:(1)由题意: 的定义域为
的定义域为 ,且
,且 .
.
 ,故
,故 在
在 上是单调递增函数. (2分)
上是单调递增函数. (2分)
(2)由(1)可知:
① 若 ,则
,则 ,即
,即 在
在 上恒成立,此时
上恒成立,此时 在
在 上为增函数,
上为增函数,
 (舍去). (4分)
(舍去). (4分)
② 若 ,则
,则 ,即
,即 在
在 上恒成立,此时
上恒成立,此时 在
在 上为减函数,
上为减函数,
 (舍去). (6分)
(舍去). (6分)
③ 若 ,令
,令 得
得 ,
,
当 时,
时, 在
在 上为减函数,
上为减函数,
当 时,
时, 在
在 上为增函数,
上为增函数,
 (9分)
(9分)
综上可知: . (10分)(3)
. (10分)(3) .
.
又 (11分)
(11分)
令 ,
,
 在
在 上是减函数,
上是减函数, ,即
,即 ,
,
 在
在 上也是减函数,
上也是减函数, .
.
令 得
得 ,∴当
,∴当 在
在 恒成立时,
恒成立时, .(14分)
.(14分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com