
题目列表(包括答案和解析)
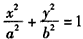 (a>b>0),A(0,b) 、B(0,-b)和 Q(a,0)为Γ的三个顶点。
(a>b>0),A(0,b) 、B(0,-b)和 Q(a,0)为Γ的三个顶点。 ,求点M的坐标;
,求点M的坐标; ,证明:E为CD的中点;
,证明:E为CD的中点; ?令a=10,b=5,点P的坐标是(-8,-1)。若椭圆Γ上的点P1、P2满足
?令a=10,b=5,点P的坐标是(-8,-1)。若椭圆Γ上的点P1、P2满足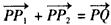 ,求点P1、P2的坐标。
,求点P1、P2的坐标。 (a>b>0),A(0,b),B(0,-b)和 Q(a,0)为Γ的三个顶点。
(a>b>0),A(0,b),B(0,-b)和 Q(a,0)为Γ的三个顶点。 ,求点M的坐标;
,求点M的坐标; ,证明:E为CD的中点;
,证明:E为CD的中点; ?令a=10,b=5,点P的坐标是(-8,-1)。若椭圆Γ上的点P1,P2满足
?令a=10,b=5,点P的坐标是(-8,-1)。若椭圆Γ上的点P1,P2满足 ,求点P1,P2的坐标。
,求点P1,P2的坐标。 =0与点D有公共点,试求a的最小值。
=0与点D有公共点,试求a的最小值。 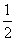 x2上一点,直线l过点P且与抛物线C交于另一点Q,
x2上一点,直线l过点P且与抛物线C交于另一点Q,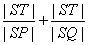 的取值范围。
的取值范围。 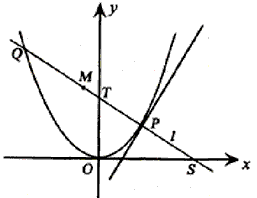
 x2上一点,直线l过点P且与抛物线C交于另一点Q,
x2上一点,直线l过点P且与抛物线C交于另一点Q, 的取值范围。
的取值范围。 
一、选择题:本小题共10小题,每小题5分,共50分.
题号
1
2
3
4
5
6
7
8
9
10
答案
B
D
B
C
A
C
B
B
A
A
二、填空题:本小题11―13题必答, 14、15小题中选答1题,若全答只计14题得分,共20分.
11. 35 12.  13.
13. 
14.
 或
或 15.
15. 

三、解答题:共80分.
16题(本题满分13分)
解:(1)要使f(x)有意义,必须 ,即
,即
得f(x)的定义域为 ………………………………7分
………………………………7分
(2)因f(x)的定义域为 ,关于原点不对称,所以
,关于原点不对称,所以
f(x)为非奇非偶函数. ……………………………………………13分
17题(本题满分13分)
解:(1)当且仅当 时,方程组有唯一解.因
时,方程组有唯一解.因 的可能情况为
的可能情况为 三种情况………………………………3分
三种情况………………………………3分
而先后两次投掷骰子的总事件数是36种,所以方程组有唯一解的概率
 ……………………………………………………………………6分
……………………………………………………………………6分
(2)因为方程组只有正数解,所以两直线的交点在第一象限,由它们的图像可知
 ………………………………………………………………9分
………………………………………………………………9分
解得(a,b)可以是(1,4),(1,5),(1,6),(2,1),(2,2),(3,1),(3,2),(4,1),(4,2),(5,1),(5,2),(6,1),(6,2),所以方程组只有正数解的概率 ………………………………………………………………………13分
………………………………………………………………………13分
18题(本题满分14分)
(1) 证明:由题设知,FG=GA,FH=HD
所以GH
 .
.
又BC
 ,故GH
,故GH BC
BC
所以四边形BCHG是平等四边形。……………………4分
(2) C、D、F、E四点共面。理由如下:
由BE
 ,G是FA的中点知,
,G是FA的中点知,
BE GF,所以EF//BG。……………………6分
GF,所以EF//BG。……………………6分
由(1)知BG//CH,故EF//CH,故F、E、C、H共面,又点D在直线FH上,
所以C、D、F、E四点共面。……………………8分
(3)
证明:连结EG,由AB=BE,BE AG,及
AG,及 ,知ABEG是正方形,
,知ABEG是正方形,
故BG⊥EA。由题设知,FA、AD、AB两两垂直,故AD⊥平面FABE,因此AD⊥BG,又EA∩AD=A,所以BG⊥平面ADE。
由(1)知,CH//BG,所以CH⊥平面ADE,由(2)知H 平面CDE,故CH
平面CDE,故CH 平面CDE,得平面ADE⊥平面CDE。……………………14分
平面CDE,得平面ADE⊥平面CDE。……………………14分
19题(本题满分14分)
解:(1)由已知得 ,解得:
,解得: ……………………4分
……………………4分
所求椭圆方程为 ………………………………………………6分
………………………………………………6分
(2)因点 即A(3,0),设直线PQ方程为
即A(3,0),设直线PQ方程为 ………………8分
………………8分
则由方程组 ,消去y得:
,消去y得:
设点 则
则 ……………………11分
……………………11分
因 ,得
,得 ,
,
又 ,代入上式得
,代入上式得
 ,故
,故
解得: ,所求直线PQ方程为
,所求直线PQ方程为 ……………………14分
……………………14分
20题(本题满分14分)
解:(1)函数f(x)的定义域为 ,
, …………2分
…………2分
①当 时,
时, >0,f(x)在
>0,f(x)在 上递增.………………………………4分
上递增.………………………………4分
②当 时,令
时,令 得
得 解得:
解得:
 ,因
,因 (舍去),故在
(舍去),故在 上
上 <0,f(x)递减;在
<0,f(x)递减;在 上,
上, >0,f(x)递增.……………8分
>0,f(x)递增.……………8分
(2)由(1)知 在
在 内递减,在
内递减,在 内递增.
内递增.
 ……………………………………11分
……………………………………11分
故 ,又因
,又因
故 ,得
,得 ………………14分
………………14分
21题(本题满分12分)
解:(1)由 ,可得
,可得
 ………………………………3分
………………………………3分
所以 是首项为0,公差为1的等差数列.
是首项为0,公差为1的等差数列.
所以 即
即 ……………………6分
……………………6分
(2)解:设 ……①
……①
 ……②
……②
当 时,①
时,① ②得
②得

 …………9分
…………9分
这时数列 的前n项和
的前n项和
当 时,
时, ,这时数列
,这时数列 的前n项和
的前n项和
 …………………………………………12分
…………………………………………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com