设P₁（x₁，y₁），P₁（x₂，y₂），…，P_n（x_n，y_n）（n≥3，n∈N） 是二次曲线C上的点，且a₁=|OP₁|²，a₂=|OP₂|²，…，a_n=|OP_n|²构成了一个公差为d（d≠0） 的等差数列，其中O是坐标原点．记S_n=a₁+a₂+…+a_n．
（1）若C的方程为

x2

9

-y²=1，n=3．点P₁（3，0） 及S₃=162，求点P₃的坐标；（只需写出一个）
（2）若C的方程为y²=2px（p≠0）．点P₁（0，0），对于给定的自然数n，证明：（x₁+p）²，（x₂+p）²，…，（x_n+p）²成等差数列；
（3）若C的方程为

x2

a2

+

y2

b2

=1（a＞b＞0）．点P₁（a，0），对于给定的自然数n，当公差d变化时，求S_n的最小值．

符号意义	本试卷所用符号	等同于《实验教材》符号
向量坐标	a ={x，y}	a =（x，y）
正切	tg	tan

已知数列{a_n}满足a1=1，an+1=an+

an2+1

，令a_n=tanθ_n(0＜θn＜

π

2

)，
求证：（1）数列{θn-

π

2

}是等比数列．
（2）a1+a2+…+an＞

(n-1)π

2

．

已知方程tan²x一tan x+1=0在x[0，n)( nN*)内所有根的和记为a_n

(1)写出a_n的表达式；(不要求严格的证明)

(2)记S_n = a₁ + a₂ +…+ a_n求S_n；

(3)设b_n =(kn一5) ，若对任何nN* 都有a_n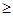b_n，求实数k的取值范围．

 

设P₁（x₁,y₁）, P₁（x₂,y₂）,…, P_n（x_n,y_n）（n≥3,n∈N） 是二次曲线C上的点, 且a₁=², a₂=², …, a_n=²构成了一个公差为d（d≠0） 的等差数列, 其中O是坐标原点. 记S_n=a₁+a₂+…+a_n.

（1）若C的方程为－y²=1,n=3. 点P₁（3,0） 及S₃=162, 求点P₃的坐标；（只需写出一个）

（2）若C的方程为y²=2px（p≠0）. 点P₁（0,0）, 对于给定的自然数n, 证明：（x₁+p）², （x₂+p）², …,（x_n+p）²成等差数列；

（3）若C的方程为（a>b>0）. 点P₁（a,0）, 对于给定的自然数n, 当公差d变化时, 求S_n的最小值.

符号意义	本试卷所用符号	等同于《实验教材》符号
向量坐标	={x,y}	=（x,y）
正切	tg	tan