
题目列表(包括答案和解析)
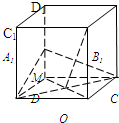 如图,正方体ABCD-A1B1C1D1中,已知O为AC与BD的交点,M为DD1的中点.
如图,正方体ABCD-A1B1C1D1中,已知O为AC与BD的交点,M为DD1的中点.正方体 棱长为1,以
棱长为1,以 为坐标原点,以直线
为坐标原点,以直线 为横轴,直线
为横轴,直线 为纵轴,直线
为纵轴,直线 为竖轴建立空间直角坐标系,如图.
为竖轴建立空间直角坐标系,如图.  为
为 的重心,
的重心,
 于
于 .(I)求点
.(I)求点 的坐标.(II)求直线
的坐标.(II)求直线 与平面
与平面 所成的角的大小.
所成的角的大小.

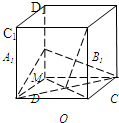 如图,正方体ABCD-A1B1C1D1中,已知O为AC与BD的交点,M为DD1的中点.
如图,正方体ABCD-A1B1C1D1中,已知O为AC与BD的交点,M为DD1的中点.如图,在正方体 中,
中,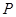 是棱
是棱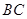 的中点,
的中点,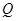 在棱
在棱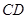 上.
上.
且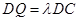 ,若二面角
,若二面角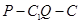 的余弦值为
的余弦值为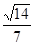 ,求实数
,求实数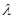 的值.
的值.
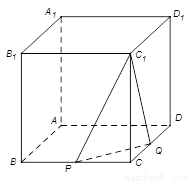
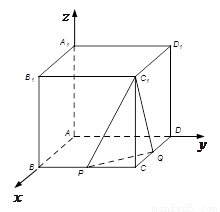
【解析】以A点为坐标原点,AB为x轴,AD为y轴,AA1为z轴,建立空间直角坐标系,设正方体的棱长为4,分别求出平面C1PQ法向量和面C1PQ的一个法向量,然后求出两法向量的夹角,建立等量关系,即可求出参数λ的值.
| 1 |
| 64 |
| 1 |
| 64 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com