
题目列表(包括答案和解析)
(本小题13分)设两向量![]() 满足
满足![]() ,
,![]() 、
、![]() 的夹角为
的夹角为![]() ,
,
(1)试求![]()
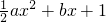 有零点的概率;
有零点的概率;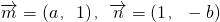 的夹角θ为锐角的概率.
的夹角θ为锐角的概率.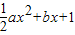 有零点的概率;
有零点的概率;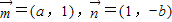 的夹角θ为锐角的概率.
的夹角θ为锐角的概率.给出下列四个命题:
①“向量,的夹角为锐角”的充要条件是“·>0”;
②如果f(x)=x,则对任意的x1、x2Î(0,+¥),且x1¹x2,都有f()>;
③设f(x)与g(x)是定义在同一区间[a,b]上的两个函数,若对任意xÎ[a,b],都有|f(x)−g(x)|£1成立,则称f(x)和g(x)在[a,b]上是“密切函数”,区间[a,b]称为“密切区间”.若f(x)=x2−3x+4与g(x)=2x−3在[a,b]上是“密切函数”,则其“密切区间”可以是[2,3];
④记函数y=f(x)的反函数为y=f −1(x),要得到y=f −1(1−x)的图象,可以先将y=f(x)的图象关于直线y=x做对称变换,再将所得的图象关于y轴做对称变换,再将所得的图象沿x轴向左平移1个单位,即得到y=f −1(1−x)的图象.其中真命题的序号是 。(请写出所有真命题的序号)
给出下列四个命题:
①“向量,的夹角为锐角”的充要条件是“·>0”;
②如果f(x)=x,则对任意的x1、x2Î(0,+¥),且x1¹x2,都有f()>;
③设f(x)与g(x)是定义在同一区间[a,b]上的两个函数,若对任意xÎ[a,b],都有|f(x)−g(x)|£1成立,则称f(x)和g(x)在[a,b]上是“密切函数”,区间[a,b]称为“密切区间”.若f(x)=x2−3x+4与g(x)=2x−3在[a,b]上是“密切函数”,则其“密切区间”可以是[2,3];
④记函数y=f(x)的反函数为y=f −1(x),要得到y=f −1(1−x)的图象,可以先将y=f(x)的图象关于直线y=x做对称变换,再将所得的图象关于y轴做对称变换,再将所得的图象沿x轴向左平移1个单位,即得到y=f −1(1−x)的图象.其中真命题的序号是 。(请写出所有真命题的序号)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com