
题目列表(包括答案和解析)
某村计划建造一个室内面积为 的矩形蔬菜温室。在温室内,沿左、右两侧与后侧内墙各保留
的矩形蔬菜温室。在温室内,沿左、右两侧与后侧内墙各保留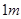 宽的通道,沿前侧内墙保留
宽的通道,沿前侧内墙保留 宽的空地,当矩形温室的边长各为多少时,蔬菜的种植面积最大?最大种植面积是多少?
宽的空地,当矩形温室的边长各为多少时,蔬菜的种植面积最大?最大种植面积是多少?
【解析】本试题考查了实际生活中的最值问题的运用,首先确定设矩形温室的长为xm,则宽为800/xm。
依题意有:种植面积: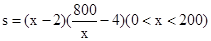
运用导数的思想得到最值。
设矩形温室的长为xm,则宽为800/xm。
依题意有:种植面积:


答:当矩形温室的长为20m,宽为40m时种植面积最大,最大种植面积是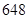 m2
m2
函数f(x)定义域为(a,b),导数![]() 在(a,b)内的图象如图,则f(x)在区间(a,b)内有极小值点 ( )
在(a,b)内的图象如图,则f(x)在区间(a,b)内有极小值点 ( )
A.1个 B.2个 C.3个 D.4个
某奇石厂为适应市场需求,投入98万元引进我国先进设备,并马上投入生产.第一年需各种费用12万元,从第二年开始,每年所需费用会比上一年增加4万元.而每年因引入该设备可获得年利润为50万元.请你根据以上数据,解决以下问题:
(1)引进该设备多少年后,该厂开始盈利?
(2)引进该设备若干年后,该厂提出两种处理方案:
第一种:年平均利润达到最大值时,以26万元的价格卖出.
第二种:盈利总额达到最大值时,以8万元的价格卖出.问哪种方案较为合算?
【解析】本试题主要考查了运用函数的思想,求解实际生活中的利润的最大值的运用。关键是设变量,表示利润函数。
一边长为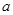 的正方形铁片,铁片的四角各截去一个边长为
的正方形铁片,铁片的四角各截去一个边长为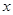 的小正方形,然后做成一个无盖方盒.
的小正方形,然后做成一个无盖方盒.
(Ⅰ)试把方盒的体积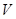 表示为
表示为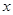 的函数;
的函数;
(Ⅱ)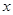 多大时,方盒的体积
多大时,方盒的体积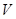 最大?
最大?
【解析】本试题主要考查了函数在实际生活中表示体积的最值的运用。
(1)提出统计假设:某种指标服从正态分布N(μ,σ2);
(2)确定一次试验中的取值a;
(3)作出统计推断:若a∈(μ-3σ,μ+3σ),则接受假设,若a![]() (μ-3σ,μ+3σ),则拒绝假设.
(μ-3σ,μ+3σ),则拒绝假设.
某砖瓦厂生产的砖的“抗断强度”ξ服从正态分布N(30,0.8),质检人员从该厂某一天生产的1 000块砖中随机抽查一块,测得它的抗断强度为27.5 kg/cm2,你认为该厂这天生产的这批砖是否合格?为什么?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com